Пример применения модифицированного МАИ
ЛПР (руководитель фирмы) должен принять решение и выбрать одного из семи кандидатов на должность начальника отдела некоторой фирмы по четырем критериям: образование (K1), опыт работы на руководящей должности (K2), результаты проведенного собеседования (тестирование) (K3), коммуникабельность (K4).
По условию задачи имеется множество альтернатив 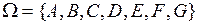 и множество критериев
и множество критериев 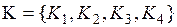 . Веса критериев соответственно равны 0,311, 0,183, 0,42, 0,086.
. Веса критериев соответственно равны 0,311, 0,183, 0,42, 0,086.
Эксперту необходимо выделить в соответствии с заданным критерием 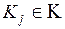 из множества критериев K некоторое подмножество или группу альтернатив
из множества критериев K некоторое подмножество или группу альтернатив 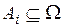 из множества альтернатив Ω (рис. 3.6) и оценить степени предпочтения выделенных групп альтернатив (табл. 3.3-3.6) в рамках заданной шкалы (1÷9). Таким образом по каждому из критериев формируются матрицы вида
из множества альтернатив Ω (рис. 3.6) и оценить степени предпочтения выделенных групп альтернатив (табл. 3.3-3.6) в рамках заданной шкалы (1÷9). Таким образом по каждому из критериев формируются матрицы вида
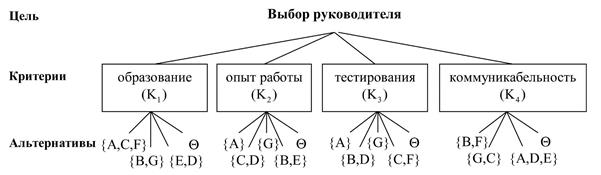
Рис. 3.6. ДШ/МАИ иерархия для примера «выбор руководителя»
Таблица 3.3
Усеченная матрица по критерию K1 – «образование»
| {A,C,F} | {E,D} | {B,G} | Ω | |
| {A,C,F} | ||||
| {E,D} | ||||
| {B,G} | ||||
| Ω | 1/5 | 1/2 | 1/4 |
Таблица 3.4
Усеченная матрица по критерию K2 – «опыт работы»
| {C,D} | {B,E} | {G} | {A} | Ω | |
| {C,D} | |||||
| {B,E} | |||||
| {G} | |||||
| {A} | |||||
| Ω | 1/2 | 1/3 | 1/5 | 1/4 |
Таблица 3.5
Усеченная матрица по критерию K3 – «тестирование»
| {B,D} | {C,F} | {G} | {A} | Ω | |
| {B,D} | |||||
| {C,F} | |||||
| {G} | |||||
| {A} | |||||
| Ω | 1/4 | 1/2 | 1/5 | 1/3 |
Таблица 3.6
Усеченная матрица по критерию K4 – «коммуникабельность»
| {A,D,E} | {B,F} | {G,C} | Ω | |
| {A,D,E} | ||||
| {B,F} | ||||
| {G,C} | ||||
| Ω | 1/5 | 1/2 | 1/3 |
Основные массы вероятности выделенных подмножеств исходного множества альтернатив Ω, по каждому из критериев, вычисляются по формуле (3.16).
Рассчитаем для каждой группы свидетельств основные массы вероятности выделенных подмножеств исходного множества альтернатив Ω:
по критерию «образование»:
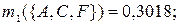
| 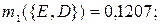
|
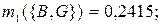
| 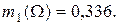
|
по критерию «опыт работы»:
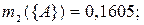
| 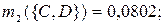
| 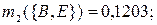
| |
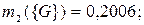
| 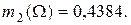
| ||
по критерию «тестирование»:
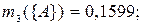
| 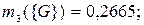
| 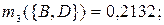
| |
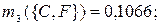
| 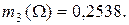
| ||
по критерию «коммуникабельность»:
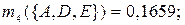
| 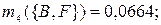
|
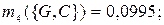
| 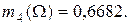
|
Скомбинируем полученные основные массы вероятностей по правилу Демпстера (3.5). Результаты комбинирования представлены в таблице 3.7.
Таблица 3.7
Дата добавления: 2021-03-18; просмотров: 527;











