Теория правдоподобных и парадоксальных рассуждений Дезера-Смарандаке (ТДС)

В основе теории свидетельств лежит следующее концептуальное положение: основу анализа (множество альтернатив) образует множество взаимно исключающих и исчерпывающих элементов (альтернатив). Это трактуется как рассмотрение всех возможных, уникально определенных и четко отличимых друг от друга элементов. Однако, на практике достичь взаимной исключаемости удается не всегда — некоторые элементы могут в значительной степени перекрываться друг другом. Поэтому выделить полностью различающиеся элементы не представляется возможным.

Математическим аппаратом, позволяющим корректно оперировать с такого рода неопределенностями, является теория правдоподобных и парадоксальных рассуждений (теория Дезера–Смарандаке, ТДС), предложенная в работах [41, 42].

ТДС рассматривает множество Ω (основа задачи) только как множество исчерпывающих элементов 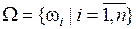. Элементы основы анализа перекрывают друг друга, соответственно условие исключаемости уже не поддерживается, и имеет место единственное предположение исчерпываемости. Ситуация, при которой невозможно уникально определить некоторые/все элементы основы анализа (вследствие чего они могут частично перекрываться), возникает из-за недостатка исходной информации

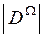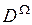Число возможных подмножеств Ω составит , где – множество всех возможных подмножеств, которые могут быть сформированы на множестве Ω, включая пустое множество Ø.

Так, например:

– при n=0, имеем 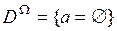и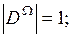

– при n=1, имеем 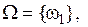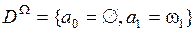и ;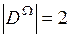

– при n=2, имеем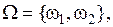

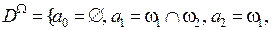
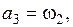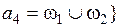, и .

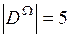На основе ТДС экспертом могут быть выделены подмножества 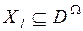(рис.3.7), 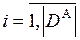, удовлетворяющие условиям:

1. Условия, которые соответствуют (3.1). 2.

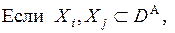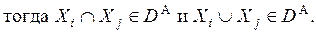
(3.18)

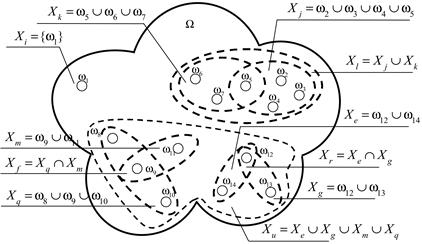
Рис. 3.7. Представление основы задачи в теории правдоподобных и парадоксальных рассуждений (теория Дезера-Смарандаке)

Таким образом, по результатам экспертного опроса может быть сформирована система подмножеств 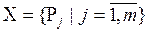, отражающая выбор всех экспертов 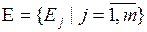, где 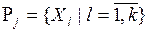- система подмножеств, сформированная экспертом E_j ( , ).

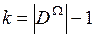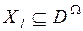Если 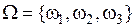, то число возможных подмножеств 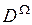составит 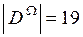. Соответственно на основе одной группы свидетельств можно выделить следующие подмножества элементов 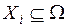, , 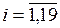что соответствует свободной модели ДС:

; ; ; ; ;

; ; ; ; ;

; ; ; ; ;

; ; ;

.

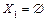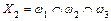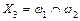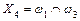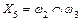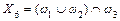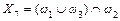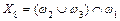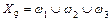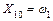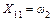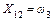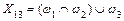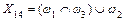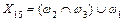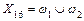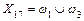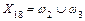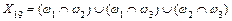Рис. 3.8. Условное представление перекрывающихся элементов

основы анализа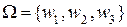

В некоторых случаях могут приниматься предположение о введении ограничений общности на некоторые элементы X_i из 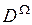(например, ограничение исключаемости, принимающее в расчет, что некоторые пересечения элементов 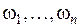невозможны, т.е. 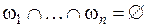). Подобная ситуация является частным случаем свободная модель ДС соответствует гибридной модели Дезера–Смарандаке.

Введем на рассмотренную ранее модель (рис. 3.8) ограничения 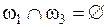и 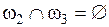, т.е. лишь элементы 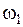и 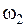перекрывают друг друга.

Рис. 3.9. Условное представление частично перекрывающихся элементов основы анализа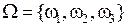

Учитывая введенные ограничения множество всех возможных подмножеств 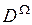составит:

; ; ;

; ; ;

; ; ;

.

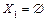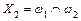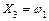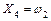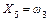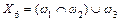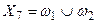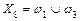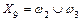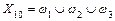Основу ТДС так же как и основу ТДШ составляют три базовые функции [41, 42] ( ):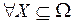

- основная масса вероятности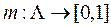

;

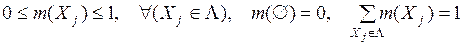- функция уверенностей (доверия :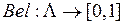

;

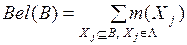- функция правдоподобия :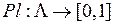

;

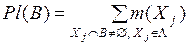где 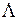соответствует .

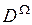Для получения агрегированной (обобщенной) оценки в рамках правдоподобных и парадоксальных рассуждений используется правило комбинирования Дезера–Смарандаке.

Это правило отображает конъюнктивный консенсус между обобщенными основными назначениями уверенностей, полученными на основе независимых групп свидетельств.

Комбинированная масса вероятности пересекающихся фокальных элементов, при условии, что 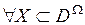, определяется выражением:

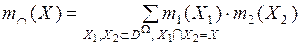, (3.19)

где m₁₂(X) – комбинированная масса вероятности для подмножества X, рассчитанная на основе конъюнктивного консенсуса.

Если уровень конфликта значителен, то для агрегирования экспертных оценок может быть применено правило комбинирования PCR5, позволяющее перераспределить конфликтные основные назначения вероятности на подмножества, вовлечённые в локальные конфликты [42].

Для случая двух групп свидетельств комбинированная масса вероятности для подмножества 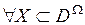согласно правилу PCR5 рассчитывается по выражению:

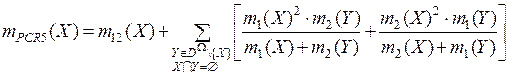(3.20)

Рассмотрим ряд примеров, иллюстрирующих различные подходы при расчете агрегированной оценки в условиях конфликтующих экспертных суждений (свидетельств).

Пример 3.2. Пусть имеется множество альтернатив (основа задачи) 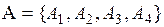и два эксперта, выполняющих их оценивание.

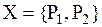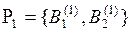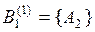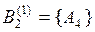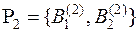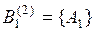В результате проведения экспертного опроса была сформирована система подмножеств , отражающая выбор экспертов 1 и 2. представляет собой множество, которое является совокупностью выделенных экспертом 1 подмножеств и . Экспертом 2 было сформировано множество , где и 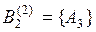. На рисунке 3.10 изображены выделенные экспертами 1 и 2 подмножества.

Выделенным подмножествам назначены основные назначения вероятности:

Эксперт 1:		;	;	;	;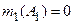
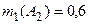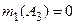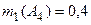Эксперт 2:		;	;	;	.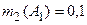

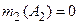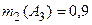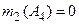Рис. 3.10. Выделенные экспертами 1 и 2 подмножества (пример 3.2)

Рассчитаем результирующее основное назначение вероятности m₁₂(·) на основе правил комбинирования Демпстера, Дезера–Смарандаке и правила PCR5. В таблице 3.10 представлены результирующие подмножества, образованные путем пересечения выделенных экспертами подмножеств.

Коэффициент конфликтности для примера 1 составил:

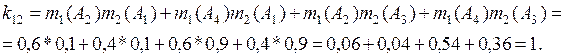
Таблица 3.10