Результирующие (комбинированные) массы вероятности
| Результирующие подмножества | Правила комбинирования свидетельств | |||
| Демпстера | Ягера | Жанга | Инагаки | |
| {A1} | 0,22018 | 0,12 | 0,1556 | 0,1746 |
| {A2} | 0,18349 | 0,1 | 0,1285 | 0,1455 |
| {A3} | 0,18349 | 0,1 | 0,2684 | 0,1455 |
| {A5} | 0,19266 | 0,105 | 0,1363 | 0,1528 |
| {A1,A2} | 0,22018 | 0,12 | 0,3112 | 0,1746 |
Учитывая тот факт, что в настоящее время предложено достаточно большое количество правил (техник) комбинирования, а также отсутствие унифицированного набора критериев, относительно которых можно однозначно оценить то или иное правило – возникает задача поиска оптимального правила для решения конкретных задач.
При выборе правила необходимо учитывать ряд факторов (критериев), относительно которых будет оценено то или иное правило комбинирования, например, модель анализа, информация о конфликтах и консенсусе между отдельными суждениями экспертов (свидетельствами), информация об источниках данных (экспертах), информация о степени взаимодействия и структуре суждений экспертов (свидетельств).
Рассмотрим процедуру выбора эффективного правила комбинирования свидетельств в зависимости от характера имеющихся данных на основе различных источников информации:
1. В случае, когда источники информации признаны надежными (в качестве меры надежности может быть рассмотрен такой критерий как компетентность экспертов), применяются правила комбинирования на основе конъюнктивного консенсуса (Демпстера, Ягера, Жанга, Инагаки).
1.1 Правило Демпстера применяется в случаях:
1.1.1. Суммарное значение всех назначений вероятности фокальных элементов намного больше назначения вероятности, относящейся к основе анализа (характеризующей полное незнание).
1.1.2. Имеется ситуация минимального конфликта (k≤0,3) между отдельными группами свидетельств.
1.1.3. Суждения экспертов являются согласованными (сформированные экспертами подмножества 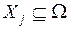 ,
, 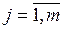 , подчинены условию:
, подчинены условию: 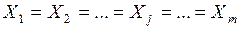 ).
).
1.2 Правило Жанга применяется в случаях:
1.2.1. Суммарное значение всех назначений вероятности фокальных элементов намного больше или сопоставимо с назначением вероятности, относящимся к основе анализа.
1.2.2. Имеется ситуация некоторого конфликта (k≤0,5) между отдельными группами свидетельств.
1.2.3. Суждения экспертов являются согласованными.
1.3 Правило Инагаки применяется в случаях:
1.3.1. Назначение вероятности, относящееся основе анализа больше или сопоставимо с назначением вероятности всех фокальных элементов.
1.3.2. Имеется ситуация некоторого конфликта (k≤0,5) между отдельными группами свидетельств.
1.3.3. Нет никакой информации о степени пересечения различных свидетельств (фокальных элементов).
1.4 Правило Ягера применяется в случаях:
1.4.1. Суммарное значение всех назначений вероятности фокальных элементов сопоставимо с назначением вероятности, относящимся к основе анализа.
1.4.2. Имеется ситуация существенного конфликта (k≤0,7) между отдельными группами свидетельств.
1.4.3. Суждения экспертов являются сопоставимыми (сформированные экспертами подмножества 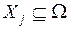 ,
, 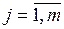 , подчинены условию:
, подчинены условию: 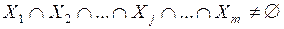 ).
).
2. В случае, когда известно, что некоторые из источников признаны ненадежными, но не известно, какие именно, то реккомендуется применять правила на основе дизъюнктивного консенсуса (правило х–свертывающегося усреднения, дизъюнктивное правило Дюбуа и Прада).
3. В случае, когда известно, какие именно из источников являются ненадежные, такие источники исключаются из рассмотрения.
4. Если все источники признаны ненадежными, необходимо пополнить информацию из других источников, которые могут считаться надежными. В этом случае меняется состав экспертной комиссии, и экспертиза проводится повторно.
Схематически обобщенный алгоритм выбора правила комбинирования представлен на рис. 3.5.
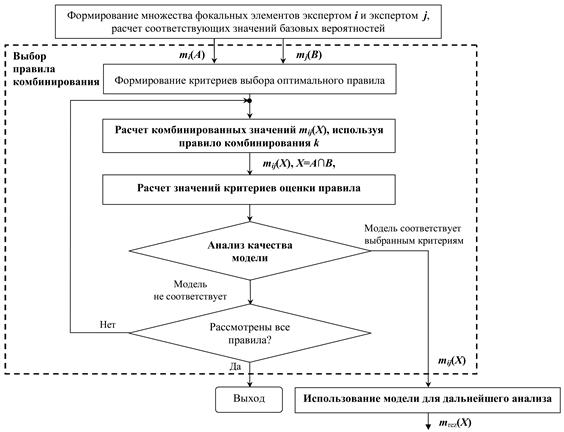
Рис. 3.5. Обобщенный алгоритм выбора правила комбинирования
Дата добавления: 2021-03-18; просмотров: 511;











