Степень пересечения выделенных экспертами подмножеств (пример 3.1)

	Эксперт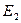
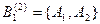
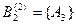
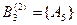
Эксперт

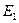
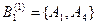
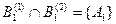
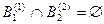
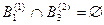
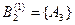
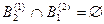
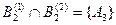
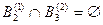
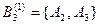
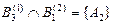
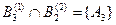
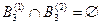
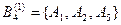
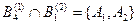
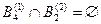
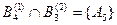
Рассчитаем результирующее значения массы вероятности m₁₂(·) на основе правил комбинирования Демпстера, Ягера, Жанги и Инагаки.

Коэффициент конфликтности K вычисляется (3.6), исходя из того, что

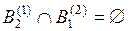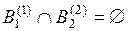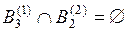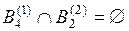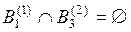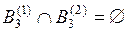, , , , и , т.е.

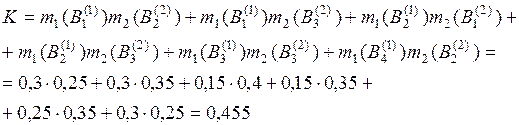
Отсюда 1 – K = 1 – 0,455 = 0,545.

Рассчитаем комбинированные значения масс вероятности для пересечений маргинальных подмножеств (фокальных элементов) основы анализа А:

по правилу Демпстера (3.5)

.

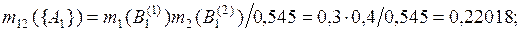
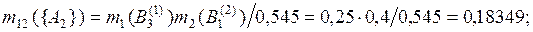
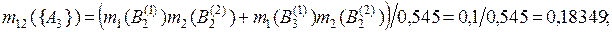
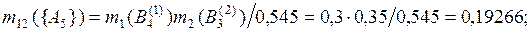
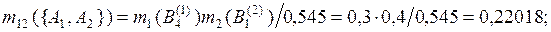
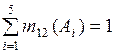по правилу Ягера(3.7):

.

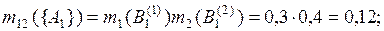
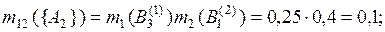
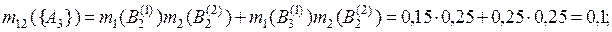
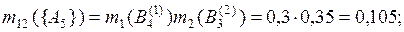
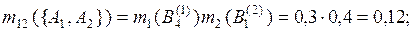
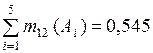по правилу Жанга(3.10):

По выражению (3.9) рассчитаем значения степеней пересечения соответствующих подмножеств:

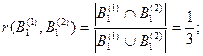
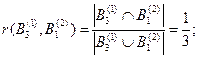
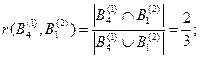
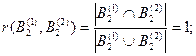
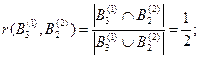
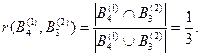
Рассчитаем промежуточные оценки m₁₂(·) по правилу комбинирования Жанга (без учета коэффициента нормализации):

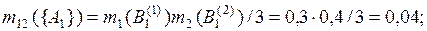
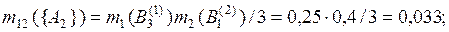
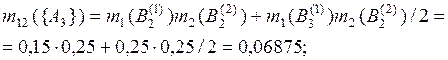
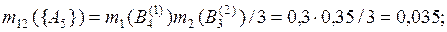
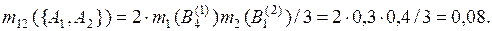
Сумма всех результирующих масс вероятности равна 0,25675. Чтобы рассчитать комбинированные значения масс вероятности по выражению (3.10), примем значение константы нормализации Κ равным

.

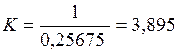Умножая рассчитанные ранее промежуточные оценки m₁₂(·) на значение Κ, окончательно имеем

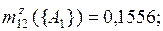
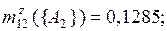
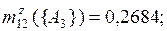
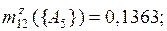
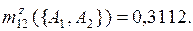
по правилу Инагаки(3.11):

Стандартным образом скомбинируем маргинальные основные массы вероятности:

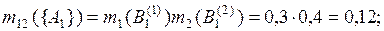
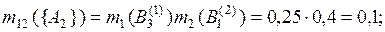
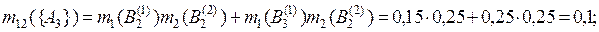
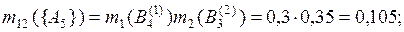
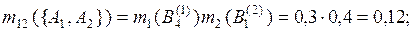
Суммируя массы вероятности в ячейках табл. 3.1 для пустых пересечений маргинальных фокальных элементов, имеем

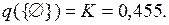
Применим правило комбинирования Инагаки (3.11) к полученным промежуточным результатам.

При k = 0

.

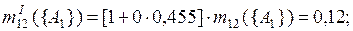
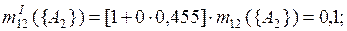
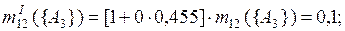
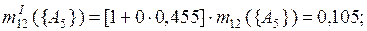
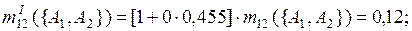
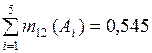В этом случае полученные результаты соответствуют результатам комбинирования по правилу Ягера.

При k = 1

.

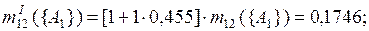
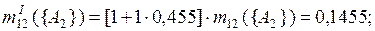
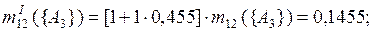
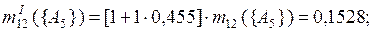
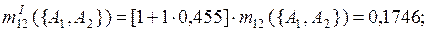
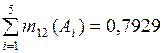Сумма комбинированных масс вероятности меньше 1. Такой результат обусловлен тем, что значение нормализующей константы k = 1 меньше, чем 1/(1–q(Ø))=1,835, что соответствует комбинированию по правилу Демпстера.

При k = 1,835

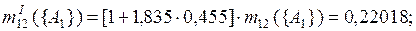
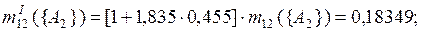
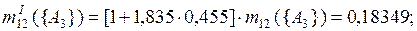
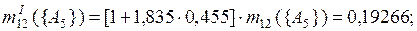
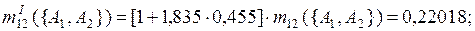
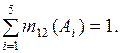
Различия между результатами при использовании разных правил комбинирования связаны с применением разных подходов при комбинировании основных масс вероятности исходных фокальных элементов, в основном в обращении с комбинированными массами уверенностей для пустых пересечений исходных фокальных элементов.

Таблица 3.2