Описание модифицированного метода МАИ

Пусть имеется множество альтернатив и множество критериев .

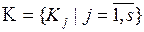Метод состоит из следующих этапов:

1. Выявление предпочтений эксперта. Эксперт, в соответствии с заданным критерием выделяет некоторое подмножество или группу 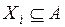альтернатив из множества альтернатив А(из всего множества альтернатив подмножество X_i для эксперта является наиболее предпочтительным), таким образом формируя систему подмножеств 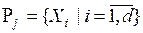, , 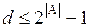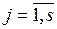. Соответственно, экспертом будет сформировано s множеств P_j, отражающих его выбор по каждому из критериев , .

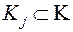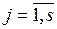2. Расчет вектора приоритетов критериев 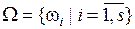, например, используя один из способов, приведенных в [35]:

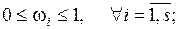
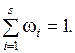
Приоритеты между критериями устанавливаются по степени их влияния на выбор варианта (альтернативы).

3. Выявление степени превосходства выделенных групп элементов (альтернатив) X_i в значениях заданной шкалы предпочтений по каждому из критериев. Для этого строятся так называемые усеченные матрицы парных сравнений, в которых элементы главной диагонали равны единицам, элементы крайнего правого столбца и нижней строки матрицы характеризуют степени b_i предпочтений вида (крайний справа столбец) или 1/b_i предпочтений 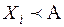(нижняя строка), все остальные элементы равны нулю.

Таким образом, для каждой системы подмножеств 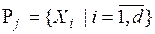будет сформирован вектор 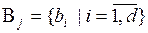, который содержит численные значения степеней предпочтения b_i вида 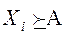, , 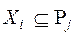выделенных экспертом по критерию K_j.

4. Вычисление основных масс вероятностей, соответствующих выделенным подмножествам (группам элементов) X_i. Для каждой сформированной системы подмножеств 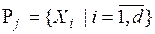будет получен вектор 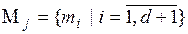, элементы которого вычисляются по формулам [38]:

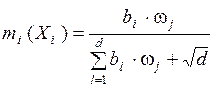, (i= 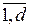), , 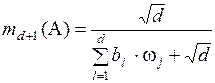(3.16)

где d – общее число выделенных подмножеств (групп элементов) X_i экспертом по критерию K_j; b_i – степень предпочтения X_i ( 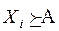), назначенная экспертом по критерию K_j; ω_j – весовой коэффициент (приоритет) критерия K_j; m_i(X_i) – основная масса вероятности, назначенная множеству X_i; m_d+1(A) – основная масса вероятности, назначенная основе анализа А. Значение, соответствующее m_d+1(A), отражает степень полного незнания эксперта относительно критерия K_j.

5. Комбинирование полученных основных масс вероятностей 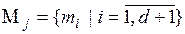выделенных экспертом по критериям K_j, 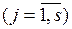, таким образом, будет выполнено s–1 операция комбинирования. При этом оценки эксперта принимаются за независимый источник информации; в качестве правила комбинирования используется правило комбинирования Демпстера.

Результатом комбинирования является множество 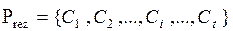, , 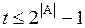содержащее результирующие подмножества, полученные путем комбинирования P_i и P_j, 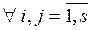и вектор 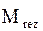, содержащий основные массы вероятностей 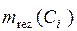результирующих подмножеств C_i.

6. Расчет значений функции доверия Bel(·) и правдоподобия Pl(·). Расчет указанных функций производится для каждого подмножества C_i, используя формулы (3.3) и (3.4). Установление приоритета подмножества C_i осуществляется путем сравнения полученных интервалов [Bel({C_i}),Pl({C_i})], образованных функциями доверия и правдоподобия. Лучшим считается тот элемент (подгруппа элементов основы анализа), у которого значение функции доверия и правдоподобия являются наибольшими среди аналогичных значений всех остальных интервалов. В случае, когда рассматриваемые интервалы являются вложенными, то их сравнение выполняется с использованием выражения:

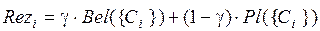, (3.17)

где γÎ[0,1] – коэффициент оптимизма.

Главным преимуществом предложенной методики является то, что в отличие от существующих методов многокритериальной оценки альтернатив, она позволяет обрабатывать оценки экспертов с несовпадающими, а возможно и противоречивыми предпочтениями по многим разнородным критериям, учитывать различные виды взаимодействия суждений (предпочтений, оценок), высказанных экспертом.