Комбинированные базовые вероятности
| Подмножество альтернатив | 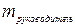
| Подмножество альтернатив | 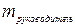
| Подмножество альтернатив | 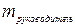
|
| {A} | 0,19262 | {G,C} | 0,00916 | {B,F} | 0,00612 |
| {B} | 0,09221 | {C,D} | 0,01126 | {A,C,F} | 0,05528 |
| {C} | 0,06236 | {B,E} | 0,01689 | {A,D,E} | 0,01528 |
| {D} | 0,05991 | {E,D} | 0,0276 | Ω | 0,06154 |
| {E} | 0,01177 | {B,G} | 0,04423 | ||
| {F} | 0,00806 | {C,F} | 0,02585 | ||
| {G} | 0,24819 | {B,D} | 0,0517 |
По комбинированным основным назначения вероятностей вычислим функции доверия Bel({Ai}) и правдоподобия Pl({Ai}) для каждой исходной альтернативы (табл. 3.8).
Таблица 3.8
Значения функций доверия и правдоподобия для исходного множества альтернатив
| Подмножество альтернатив | bel(×) | pl(×) | Подмножество альтернатив | bel(×) | pl(×) |
| {A} | 0,19262 | 0,32471 | {E} | 0,01177 | 0,13307 |
| {B} | 0,09221 | 0,27268 | {F} | 0,00806 | 0,15684 |
| {С} | 0,06236 | 0,22545 | {G} | 0,24819 | 0,36312 |
| {D} | 0,05991 | 0,22728 |
Из приведенных результатов видно, что наибольшие значения функции доверия и правдоподобия имеет выбор G, но однозначно определить результирующую ранжировку альтернатив невозможно, поскольку полученные интервалы являются вложенными. Для определения степени превосходства исходных альтернатив введем коэффициент пессимизма γ=0,6 и рассчитаем значение  для каждой исходной альтернативы (3.17).
для каждой исходной альтернативы (3.17).
Таблица 3.9
| Альтернатива | {A} | {B} | {С} | {D} | {E} | {F} | {G} |
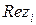
| 0,2455 | 0,1644 | 0,1276 | 0,1269 | 0,0603 | 0,0676 | 0,2942 |
В результате анализа получим следующую ранжировку альтернатив:
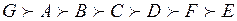 .
.
Дата добавления: 2021-03-18; просмотров: 586;











