Степень пересечения выделенных экспертами подмножеств (пример 3.2)
| Эксперт 1 | |||
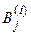
| 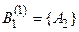
| 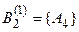
| |
| Эксперт 2 | 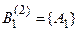
| 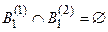
| 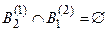
|
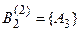
| 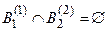
| 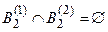
|
При такой ситуации применение правила Демпстера невозможно т.к. уровень конфликта равен 1.
На основе классического правила комбинирования Дезера–Смарандаке выделены результирующие подмножества:
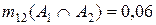 ;
; 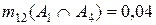 ;
;
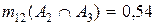 ;
; 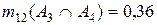 ;
; 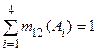 .
.
Как видно из таблицы 3.10 в модели имеются 4 локальных конфликта: A1ÇA2=Ø, A1ÇA4=Ø, A2ÇA3=Ø, A3ÇA4=Ø. Суммарное значение которых составляет 1.
Первый локальный конфликт m12(A1ÇA2)=m1(A2)m2(A1)= =0,6*0,1=0,06 пропорционально распределяется между выбором A1 и A2 в соответствии с выражением
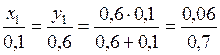 .
.
Тогда x1= (0,06*0,1)/0,7=0,0086; y1= (0,06*0,6)/0,7=0,0514.
Второй локальный конфликт m12(A1ÇA4)=m1(A4)m2(A1)=0,04 пропорционально распределяется между выбором A1 и A4 в соответствии с выражением
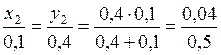 .
.
Тогда x2= (0,04*0,1)/0,5=0,008; y2= (0,04*0,4)/0,5=0,032.
Третий локальный конфликт m12(A2ÇA3)=m1(A2)m2(A3)= =0,6*0,9=0,54 пропорционально распределяется между выбором A2 и A3 в соответствии с выражением
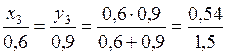 .
.
Тогда x3= (0,54*0,6)/1,5=0,216; y3= (0,54*0,9)/1,5=0,324.
Четвертый локальный конфликт m12(A3ÇA4)=m1(A4)m2(A3)= =0,4*0,9=0,36 пропорционально распределяется между выбором A3 и A4 в соответствии с выражением
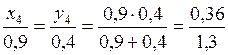 .
.
Тогда x4= (0,36*0,9)/1,3=0,249; y4= (0,36*0,4)/1,3=0,111.
Результирующие основные назначения вероятности в соответствии с правилом PCR5:
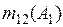 =0+0,0086+0,008=0,0166; =0+0,0086+0,008=0,0166;
| 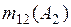 =0+0,0514+0,216=0,2674; =0+0,0514+0,216=0,2674;
|
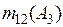 =0+0,324+0,249=0,573; =0+0,324+0,249=0,573;
| 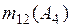 =0+0,032+0,111=0,143. =0+0,032+0,111=0,143.
|
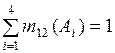 .
.
Полученные результаты дают возможность сформулировать следующие утверждения:
1. Правило комбинирования Демпстера относит назначения вероятности, связанные с конфликтующими подмножествами, к пустому множеству и использует их только для нормализации полученных результатов. В случае значительного конфликта это приводит к некорректным (неправдоподобным) результатам.
2. Правило комбинирования Дезера–Смарандаке показывает лучшие результаты по сравнению с правилом Демпстера, так как позволяет получать более полную информацию о характере взаимодействия экспертных суждений (в процессе анализа образуются результирующие подмножества экспертных суждений не только на основе операции 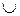 , как в теории свидетельств, но и при помощи операции
, как в теории свидетельств, но и при помощи операции 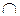 ), а также корректно обращаться с неопределенными (эксперт затрудняется с выбором), парадоксальными и противоречивыми данными (экспертными суждениями). Классическое правило комбинирования Дезера–Смарандаке позволяет обрабатывать экспертные суждения в ситуации, когда конфликтная масса уверенности достигает 1, но при этом возможна ситуация при которой не будет выделено результирующих одноэлементных подмножеств соответствующих исходным альтернативам.
), а также корректно обращаться с неопределенными (эксперт затрудняется с выбором), парадоксальными и противоречивыми данными (экспертными суждениями). Классическое правило комбинирования Дезера–Смарандаке позволяет обрабатывать экспертные суждения в ситуации, когда конфликтная масса уверенности достигает 1, но при этом возможна ситуация при которой не будет выделено результирующих одноэлементных подмножеств соответствующих исходным альтернативам.
3. Правило комбинирования PCR5 перераспределяет основное назначение вероятности, отнесенное к пустому множеству, на подмножества, вовлечённые в конфликт, пропорционально основным назначениям вероятности этих подмножеств.
Правило перераспределения конфликтов PCR5 может быть применено в ситуациях:
3.1. Имеется ситуация высокого (k≤0,9), очень высокого (0,9≤k<1) и абсолютного (k=1) конфликта между отдельными группами свидетельств. При этом будут рассчитаны комбинированные основные назначения вероятности для всех выделенных экспертами подмножеств, включая одноэлементные.
3.2. Правило не зависит от структуры экспертных суждений, и способно обрабатывать несвязанные экспертные суждения ( 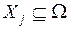 ,
, 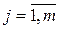 , подчинены условиям: 1)
, подчинены условиям: 1) 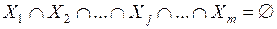 ,
, 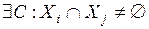 ; 2) подмножества
; 2) подмножества 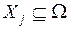 ,
, 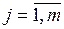 , подчинены условию:
, подчинены условию: 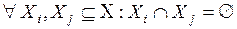 ).
).
Дата добавления: 2021-03-18; просмотров: 588;











