Закон распределения случайной функции
Рассмотрим случайную величину  – сечение случайной функции в момент t (рис. 13.1). Эта случайная величина, очевидно, обладает законом распределения, который, в общем случае, зависит от t, обозначим его
– сечение случайной функции в момент t (рис. 13.1). Эта случайная величина, очевидно, обладает законом распределения, который, в общем случае, зависит от t, обозначим его 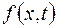 . Функция
. Функция 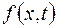 называется одномерным законом распределения случайной функции
называется одномерным законом распределения случайной функции  . Очевидно, что функция
. Очевидно, что функция 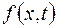 не является полной, исчерпывающей характеристикой случайной функции
не является полной, исчерпывающей характеристикой случайной функции  . Действительно, эта функция характеризует только закон распределения
. Действительно, эта функция характеризует только закон распределения  для данного, хотя и произвольного t; она не отвечает на вопрос о зависимости случайных величин
для данного, хотя и произвольного t; она не отвечает на вопрос о зависимости случайных величин  при различных t. С этой точки зрения более полной характеристикой случайной функции
при различных t. С этой точки зрения более полной характеристикой случайной функции  является так называемый двумерный закон распределения:
является так называемый двумерный закон распределения:
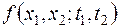 . (13.1)
. (13.1)
Это – закон распределения системы двух случайных величин 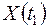 ,
, 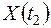 ,т.е. двух произвольных сечений случайной функции
,т.е. двух произвольных сечений случайной функции  . Однако и эта характеристика в общем случае не является исчерпывающей; еще более полной характеристикой был бы трехмерный закон:
. Однако и эта характеристика в общем случае не является исчерпывающей; еще более полной характеристикой был бы трехмерный закон:
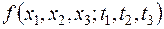 . (13.2)
. (13.2)
Очевидно, теоретически можно неограниченно увеличивать число аргументов и получать при этом все более подробную, все более исчерпывающую характеристику случайной функции, но оперировать со столь громоздкими характеристиками, зависящими от многих аргументов, крайне неудобно.
Большое применение нашли случайные функции, величины которых при любых значениях аргументов подчинены нормальному закону.
В этом случае многомерный закон распределения нормальной случайной функции может быть записан по аналогии с многомерным законом распределения системы случайных величин, подчиняющихся нормальному закону распределения (13.l). При этом в выражении (13.1) вместо математических ожиданий 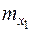 ,
, 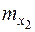 ,
, 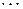 ,
, 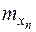 случайных величин необходимо подставить значения математического ожидания
случайных величин необходимо подставить значения математического ожидания 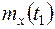 ,
, 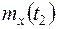 ,
, 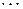 ,
, 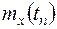 случайной функции
случайной функции  при соответствующих значениях аргумента
при соответствующих значениях аргумента 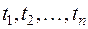 ; вместо корреляционных моментов
; вместо корреляционных моментов 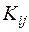 – значения корреляционной функции
– значения корреляционной функции
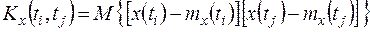 , (13.3)
, (13.3)
вместо дисперсий 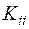 дисперсию
дисперсию 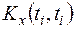 .
.
Таким образом, математические ожидания, дисперсии и корреляционные функции дают возможность в случае нормальных случайных функций полностью определить их законы распределения при любых значениях аргумента t и любом 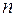 .
.
Дата добавления: 2016-12-09; просмотров: 2095;











