Оценка параметров тренда

Основой для методики оценки параметров тренда служит метод наименьших квадратов, который даёт оценки параметров, отвечающие принципу максимального правдоподобия: сумма квадратов отклонений фактических уровней от тренда должна быть минимальной для данного типа уравнения.

Предположим, что уравнение тренда имеет вид параболы:

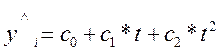. (14.8)

Т.е., 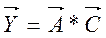(14.9)

Для вычисления параметров c₀, c₁, c₂ по методу наименьших квадратов воспользуемся формулой:

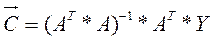, (14.10)

Все расчеты произведем в программе MS Excel. В нашем случае матрица А имеет вид

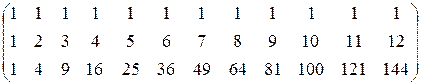
Для расчета по формуле (14.10) в программе MS Excel необходимо воспользоваться формулами ТРАНСП(массив) – для транспонирования матриц, МУМНОЖ (массив) – для перемножения матриц, МОБР(массив) – для обращения матриц.

В результате искомые коэффициенты 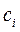будут равны: 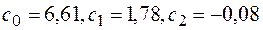. Таким образом, уравнение тренда примет вид:

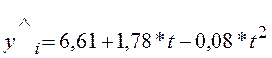. (14.11)

Изобразим теперь в одной координатной плоскости исходный ряд и ряд, полученный аналитическим выравниванием по параболе второго порядка (рис. 14.2).

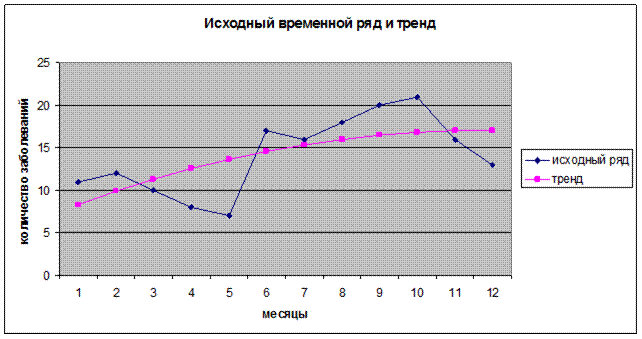
Рис. 14.2. Исходный ряд и тренд

Сезонные колебания

Если колебания временного ряда носят строго периодический или близкий к нему характер и завершаются в течение одного года, то их называют сезонными колебаниями.

Прежде чем анализировать сезонные составляющие каждого года (или какого-то другого промежутка времени), необходимо их центрировать (отклонение от среднего значения ряда).

Если взять данные заболевания пневмонией за 3 года (36 месяцев), то график будет иметь следующий вид

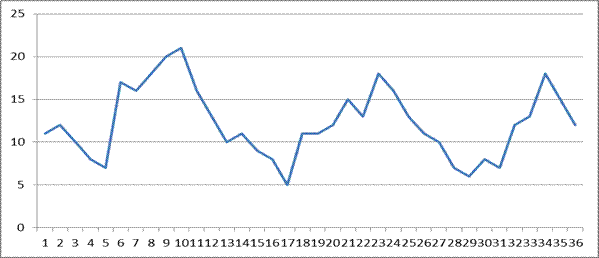
Рис. 14. 3. Случаи заболевания пневмонией за 3 года.

Видно, что в целом заболевание носит сезонный характер. За сезонную волну возьмем период с 1 по 12 месяц.

Найдём среднюю сезонную составляющую, графическая интерпретация которой имеет вид, представленный на рис. 14.3.

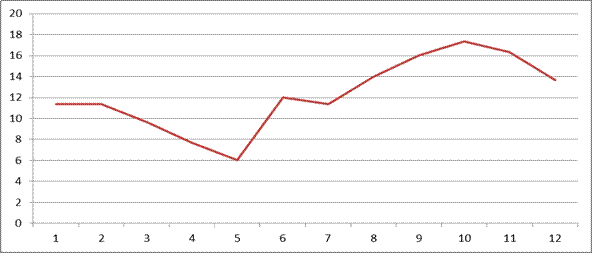
Рис. 14.4. Средняя сезонная составляющая

Поскольку нам известны значения средней сезонной волны, то мы можем неограниченно распространить её вправо и влево. В результате получим следующую зависимость (рис. 14.4).

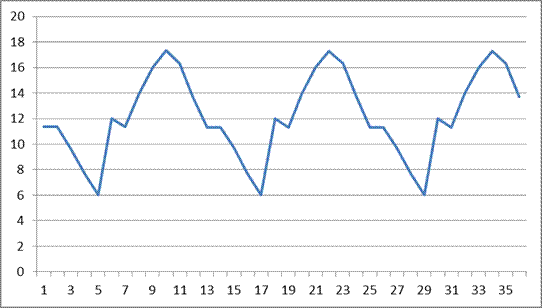
Рис. 14.5. Значения средней сезонной волны

Прогнозирование

Прогноз (в переводе с греческого языка – предвидение, предсказание, предзнание) – неотъемлемая составляющая всей человеческой деятельности, в том числе медицинской. Это промежуточное звено между познанием объективной реальности и деятельностью людей по её преобразованию.

При прогнозировании будем учитывать как тренд, так и сезонную составляющую, т.е.:

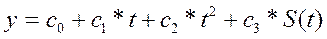, (14.12)

где S(t) – средняя сезонная составляющая. При расчёте коэффициентов 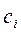будем использовать метод наименьших квадратов. В матричном виде:

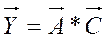. (14.13)

Искомая матрица коэффициентов 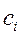будет равна:

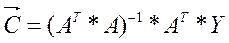. (14.14)