Построение кратчайшего остовного дерева. Алгоритм Прима в табличной форме.
По заданному графу заполняется матрица весов W(N, N). Веса несуществующих ребер предполагаются сколь угодно большими. Образуется массив P(N) меток вершин графа (столбцов матрицы весов). Алгоритм решения задачи заключается в последовательном заполнении массива меток столбцов и состоит из следующих этапов.
Предварительный этап. Обнуляется массив P(N) меток столбцов таблицы. Произвольно выбранному столбцу присваивается значение метки, равной его номеру.
Этап, повторяющийся N-1 раз (общий этап). В строках, номера которых равны номерам помеченных столбцов, находится минимальный элемент среди элементов непомеченных столбцов. Столбец, в котором находится минимальный элемент, помечается меткой, номер которой равен номеру его строки. В случае, если минимальных элементов несколько, то выбирается любой. После того, как будет помечен очередной столбец, элементу, симметричному относительно главной диагонали (для многомерного графа - с ”транспонированными индексами”), присваивается сколь угодно большое значение.
Заключительный этап. Ребра, включенные в минимальное остовное дерево, определяются по меткам столбцов. Вес остовного дерева задается суммой весов входящих в него ребер.
Пример. Пусть имеется таблица с координатами (x1i, x2i) 10 точек.
| N1 | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | N10 | |
| X1 | ||||||||||
| X2 |
В системе координат (Х1ОХ2) отметим их координаты (рис.12.2).
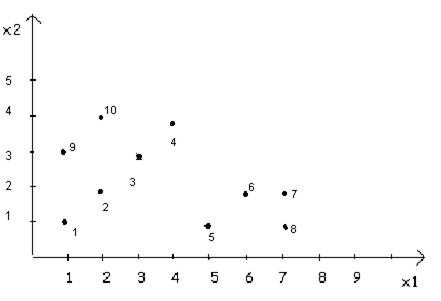
Рис. 12.2.Начальное множество точек.
Разбиение исходного графа (полученного соединением исходного множества точек) на два минимальных остовных дерева на MS Excel. В ячейках B2:K2 и B3:K3 занести координаты точек. В ячейках B5:K14 произвести подсчет расстояний между точками (рис. 12.3).
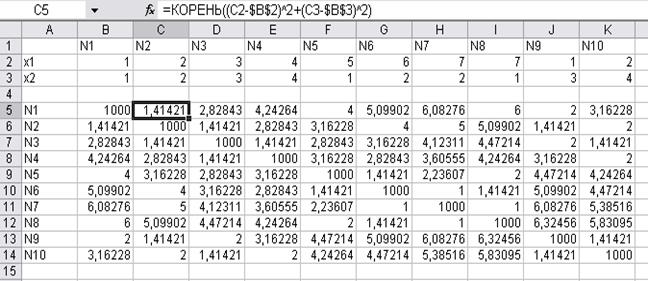
Рис.12.3. Вычисление расстояний между точками.
В двумерном пространстве расстояние между точками с координатами (x1, y1) и (x2, y2) рассчитывается по формуле 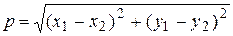 . Для n-мерного случая, когда в координатной системе (0,X1, X2, …Xn) имеются две точки с координатами (x11, x12,…, x1n) и (x21, x22, …, x2n) справедлива формула
. Для n-мерного случая, когда в координатной системе (0,X1, X2, …Xn) имеются две точки с координатами (x11, x12,…, x1n) и (x21, x22, …, x2n) справедлива формула 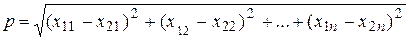 . Иногда при подсчете расстояний между точками могут учитываться веса.
. Иногда при подсчете расстояний между точками могут учитываться веса.
Рассмотрим решение задачи для двумерного случая.
На пересечении вершин с одинаковыми номерами (то есть, если i=j) поставить расстояние, равное бесконечности, или 1000. Например, формула расстояния меду вершинами 1 и 2 активизирована в строке формул. Достаточно скопировать ее (растянуть, удерживая клавишу Ctrl) по всей 5-ой строке, меняя лишь названия столбцов в относительных ссылках. Итак, должна получиться симметричная матрица А(10…10), поскольку p((xi, yj), (xk,yn)) = p((xk,yn), ( xi, yj)).
Далее построим минимальное дерево.
Для этого воспользуемся алгоритмом Прима. Над первым столбцом ставим цифру 1 и в первой строке выбираем минимальный элемент – А(1;2) = 1,41421 (ячейка С5 помечена цветом). Симметричный ему элемент заменяем бесконечностью, то есть 1000 (в ячейке B6). Значит, помечаем 2-ой столбец цифрой 1. И выбираем наименьший элемент из двух строк – 2-ой и 1-ой. Это элемент А(3;2)=1,41421 (ячейка D6). Значит, над вторым столбцом ставим цифру 2, а А(2;3)=1000 (ячейка С7). Теперь ищем минимум в 1-ой, 2-ой и 3-ей строках. Это элемент А(3;4)=1,41421 (ячейка Е7), то есть А(4;3)=1000 (ячейка D8). Помечаем 4-ый столбец цифрой 3.
Ищем минимум в 1-ой, 2-ой, 3-ей и 4-ой строках. Это элемент А(2;9)=1,41421 (ячейка J6). А(9;2)=1000. Над 9-ым столбцом ставим цифру 2.
Выбираем минимум в 1-ой, 2-ой, 3-ей, 4-ой и 9-ой строках. Это элемент А(3;10)=1,41421 (ячейка К3), то есть А(10;3)=1000. Над 10-ым столбцом ставим цифру 10.
Ищется минимум в 1-ой, 2-ой, 3-ей, 4-ой, 9-ой и 10-ой строках (напомним, что в непомеченных столбцах, то есть, в 5-ом, 6-ом, 7-ом и 8-ом). Разрешающий элемент А(3;5)=2,82843 (ячейка F7). А(5;3)=1000. Столбец 5 помечаем цифрой 3.
Выбираем минимум в строках 1, 2, 3, 4, 5, 9 и 10 (среди столбцов 6, 7, 8). Разрешающий элемент – А(5;6)=1,41421 (ячейка G5), А(6;5)=1000. 6-ой столбец помечаем цифрой 5.
Ищем минимум в строках 1, 2, 3, 4, 5, 6, 9, 10 (в столбцах 7 и 8). Минимальный элемент – А(6;8)=1,41421 (ячейка I10), А(8;6)=1000. Над 8-ым столбцом ставим цифру 6.
Наконец, в 7-ом столбце ищется минимум. Это элемент А(8;7)=1 (ячейка H12). То есть А(7;8)=1000. Помечаем 7-ой столбец цифрой 8.
Все разрешающие элементы помечены в таблице цветом. Симметричные им ячейки имеют бесконечно большое расстояние (рис. 12.4).
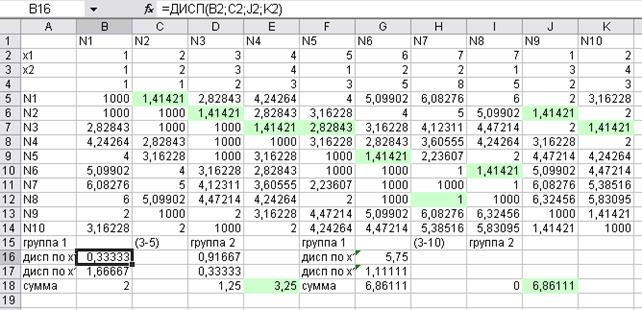
Рис. 12.4. Нахождение минимального остовного дерева и разбиение неоднородной совокупности на группы.
Таким образом, пронумерованы все столбцы, а, значит, найдены ребра минимального остовного дерева. Строки 1 и 4 указывают на соединение вершин. То есть ребрами остовного дерева являются: 1-2, 2-3, 3-5, 5-6, 7-8, 5-8, 9-2, 10-3. Вид полученного дерева представлен на рис. 12.5.
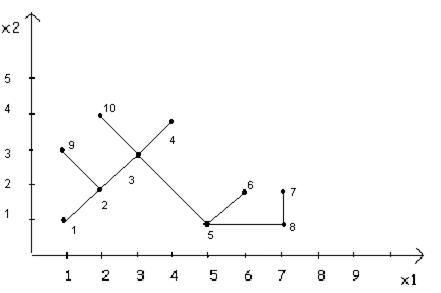
Рис. 12.5. Полученное минимальное остовное дерево.
Данный метод можно приложить и к многомерному объекту. Алгоритм остается прежним, меняется лишь формула расстояний, о которой говорилось выше.
Если рассматривается исходное неоднородное множество объектов (как в нашем случае), графически представленное в виде дерева, то для разбиения этого множества на k однородных групп необходимо удалить (k-1) ребро.
Разобьем данное дерево на два (множество точек на два подмножества, или две группы) так, чтобы суммарная дисперсия всех групп была минимальной. Для этого удалим одно из ребер – самое длинное. Из рисунка или из таблицы расстояний видно, что это ребро 3-5. Таким образом, получены 2 группы с ребрами - группа 1: 1-2, 2-3, 3-4, 9-2, 10-3 и группа 2: 5-6, 5-8, 8-7. Подсчитаем дисперсии этих групп, а затем найдем общую сумму этих дисперсий. Расчеты приведены на рис. 12.4.
Подсчитывается дисперсия по координатам х1 и х2 в 1-ой группе (ячейки B16 и B17 соответственно) и во 2-ой группе (ячейки D16 и D17) по формуле ДИСП(массив ячеек). Находятся суммы дисперсий (ячейки B18 и D18). Общая сумма дисперсий находится в ячейке Е18 (значение 3,25). Можно взять и другой вариант разбиения – исключить ребро 3-10. Группа всего 1 – исключается точка 10. Все расчеты по дисперсиям этой группы приведены в ячейках G6:I18. Сумма общей дисперсии – в ячейке J18 (6,86111). Видно, что первое разбиение оптимальнее, так как его общая дисперсия меньше.
Дата добавления: 2016-12-09; просмотров: 3552;











