Математическое ожидание, дисперсия и корреляционная функция случайной функции
Математическое ожидание случайной функции  определяется следующим образом. Рассмотрим сечение случайной функции
определяется следующим образом. Рассмотрим сечение случайной функции  при фиксированном t. Вэтом сечении мы имеем обычную случайную величину; определим ее математическое ожидание
при фиксированном t. Вэтом сечении мы имеем обычную случайную величину; определим ее математическое ожидание
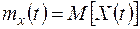 (13.4)
(13.4)
Таким образом, математическим ожиданием случайной функции  называется неслучайная функция
называется неслучайная функция 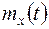 , которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
, которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
По смыслу математическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом варьируются конкретные реализации случайной функции. Величину 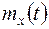 можно определять при каждом значении tкак среднее арифметическое значений реализаций случайной функции (задача 13.4).
можно определять при каждом значении tкак среднее арифметическое значений реализаций случайной функции (задача 13.4).
Аналогичным образом определяется дисперсия случайной функции. Дисперсией случайной функции  называется неслучайная функция
называется неслучайная функция 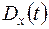 , значение которой для каждого t равно дисперсии соответствующего сечения случайной функции:
, значение которой для каждого t равно дисперсии соответствующего сечения случайной функции:
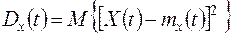 . (13.5)
. (13.5)
Дисперсия случайной функции при каждом t характеризует разброс возможных реализаций случайной функции относительно среднего, иными словами, характеризует "степень случайности" случайной функции.
Величину 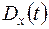 можно определить при каждом tкак среднее арифметическое значений
можно определить при каждом tкак среднее арифметическое значений 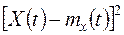 (задача 13.4). Дисперсия
(задача 13.4). Дисперсия 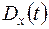 есть неотрицательная функция. Извлекая из нее квадратный корень, получаем функцию
есть неотрицательная функция. Извлекая из нее квадратный корень, получаем функцию 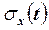 – среднее квадратическое отклонение случайной функции:
– среднее квадратическое отклонение случайной функции:
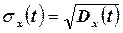 . (13.6)
. (13.6)
Степень зависимости величины 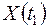 и
и 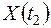 может быть в значительной мере охарактеризована их корреляционным моментом; очевидно, он является функцией двух аргументов
может быть в значительной мере охарактеризована их корреляционным моментом; очевидно, он является функцией двух аргументов 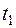 и
и 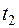 . Эта функция и называется корреляционной функцией:
. Эта функция и называется корреляционной функцией:
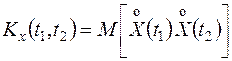 , (13.7)
, (13.7)
где 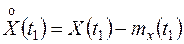 ;
;
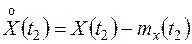 .
.
Вычисление 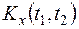 можно определить по формуле для корреляционных моментов (задача 13.4).
можно определить по формуле для корреляционных моментов (задача 13.4).
Полагая 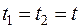 , имеем
, имеем
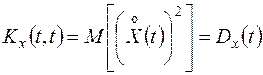 , (13.8)
, (13.8)
т.е. при 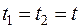 корреляционная функция обращается в дисперсию случайной функции.
корреляционная функция обращается в дисперсию случайной функции.
Рассмотрим основные свойства корреляционной функции.
1. Согласно определению (13.7) корреляционная функция симметрична относительно своих аргументов
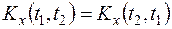 , (13.9)
, (13.9)
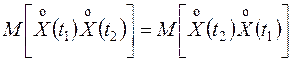 .
.
Указанное свойство можно иллюстрировать рис. 13.2.
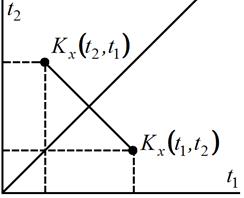
Рис. 13.2. Свойство симметричности корреляционной функции
В точках, симметричных относительно биссектрисы координатного угла, корреляционная функция имеет одинаковые значения.
Довольно часто вместо корреляционной функции 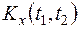 пользуются нормированной корреляционной функцией
пользуются нормированной корреляционной функцией
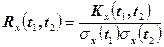 . (13.10)
. (13.10)
2. Важным свойством корреляционной функции является свойство
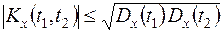 . (13.11)
. (13.11)
или
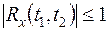 . (13.12)
. (13.12)
Нормированная корреляционная функция является безразмерной величиной, поэтому является весьма удобной в качестве оценки степени коррелированности (связности) случайных величин, задаваемых двумя сечениями случайной функции. Согласно (13.12) для наиболее тесной функциональной связи 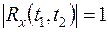 .
.
3. От прибавления к случайной функции  любой неслучайной функции
любой неслучайной функции 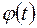 корреляционная функция не изменяется. Пусть
корреляционная функция не изменяется. Пусть 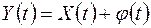 ;
; 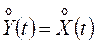 , т.е. центрированные случайные функции
, т.е. центрированные случайные функции 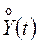 и
и 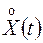 совпадают, следовательно, по определению корреляционной функции (13.7)
совпадают, следовательно, по определению корреляционной функции (13.7)
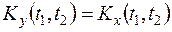 .
.
4. При умножении случайной функции функцию  на неслучайную функцию
на неслучайную функцию 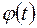 её корреляционная функция
её корреляционная функция 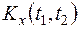 умножается на
умножается на 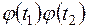 .
.
Запишем необходимые соотношения
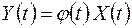 ,
, 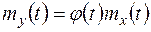 ,
, 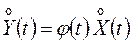 .
.
Тогда согласно (13.7) будем иметь
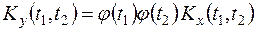 .
.
Пример 13.1. Случайная функция  задана тремя своими реализациями (рис.13.3). Найти математическое ожидание случайной функции
задана тремя своими реализациями (рис.13.3). Найти математическое ожидание случайной функции 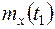 ,
, 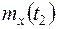 ,дисперсии случайной функции
,дисперсии случайной функции 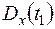 ,
, 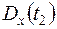 , значение корреляционной функции
, значение корреляционной функции 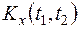 ,значение нормированной корреляционной функции
,значение нормированной корреляционной функции 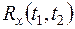 .
.
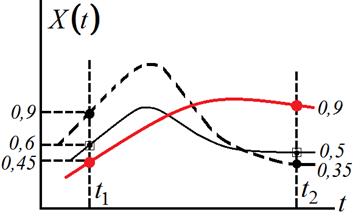
Рис. 13.3. Реализации случайной функции 
Решение. Задав сечения случайной функции 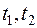 , мы имеем обычные случайные величины
, мы имеем обычные случайные величины 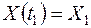 и
и 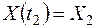 . Для большей наглядности их взаимосвязи отобразим их значения графически (рис. 13.4).
. Для большей наглядности их взаимосвязи отобразим их значения графически (рис. 13.4).
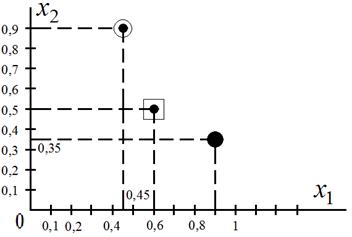
Рис. 13.4. Взаимосвязь значений случайной функции
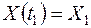 и
и 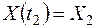
Величины 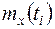 ,
, 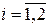 определим при каждом значении как среднее арифметическое значений реализаций случайной функции (задача 13.4)
определим при каждом значении как среднее арифметическое значений реализаций случайной функции (задача 13.4)
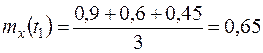 .
.
Аналогично получим 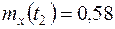 .
.
Теперь можно определить оценки значений дисперсий и среднее квадратичное отклонение (с.к.о.):
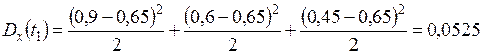 ;
;
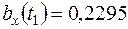 ;
;
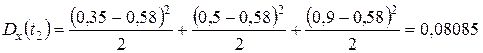 ;
;
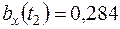 .
.
Искомая корреляционная функция 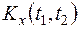 определяется как значение корреляционного момента:
определяется как значение корреляционного момента:
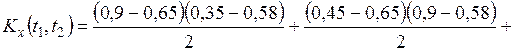
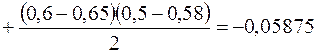 .
.
Тогда получим значение нормированной корреляционной функции
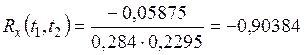 .
.
Дата добавления: 2016-12-09; просмотров: 3426;











