Взаимная корреляционная функция

Пусть на вход линейной системы с оператором L воздействует случайная функция , реакция системы представляет собой случайную функцию

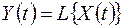. (13.16)

Отдельные реализации и 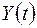представлены на рис. 13.5.

Необходимо при статистическом анализе обращать внимание на номера реализаций. Tак, реализация 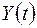под № 1 соответствует входной реализации под тем же № 1.

Взаимной корреляционной функцией двух случайных функций и 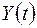называется неслучайная функция двух аргументов 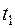и 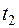, которая при каждой паре значени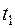й и 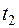равна корреляционному моменту соответствующих сечений случайной функции и случайной функции :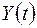

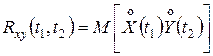. (13.17)

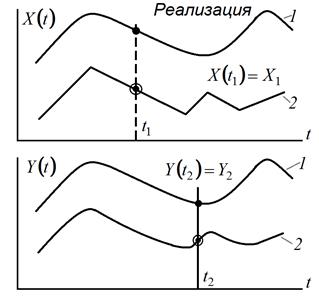
Рис. 13.5. Реализация входной случайной функции
и выходной случайной функции

Вычисление 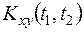можно определить по формуле для корреляционных моментов.

Рассмотрим основные свойства взаимной корреляционной функции.

1. Согласно определению (13.17) можно записать

;

.

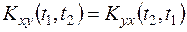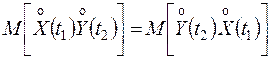Довольно часто вместо корреляционной функции 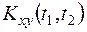пользуются нормированной взаимной корреляционной функцией

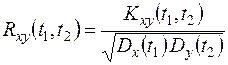. (13.18)

2. Важным свойством взаимной корреляционной функции является свойство

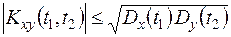(13.19)

или

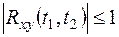. (13.20)

3. От прибавления к случайным функциям и 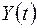неслучайных функций взаимная корреляционная функция не изменяется.

Пусть

,

.

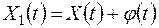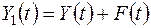тогда

,

.

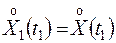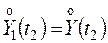следовательно,

.

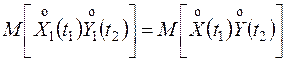4. При умножении случайной функции на неслучайную функцию 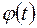, а случайной функции 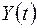на неслучайную функцию 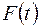взаимная корреляционная функция 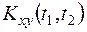умножается на .

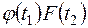Запишем необходимые соотношения:

;

;

;

;

;

.

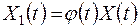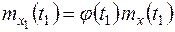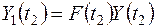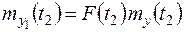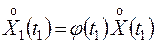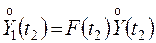Тогда согласно (13.17) будем иметь

.

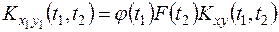Пример 13.2. Случайная функция задана тремя своими реализациями (рис.13.6), реакция линейной системы на случайную функцию представлена реализациями 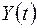(рис. 13.6).

Найти математическое ожидание случайной функции 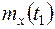, , 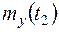дисперсии случайной функции 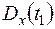, , 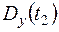значение взаимной корреляционной функции 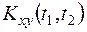, значение нормированной корреляционной функции .

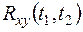Решение. Задав сечения случайных функций 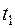, , 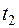получим обычные случайные величины 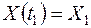и 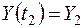. Дальнейшие расчеты проводятся аналогично расчетам из примера 13.1.

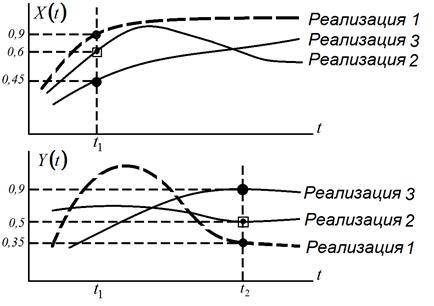
Рис. 13.6. Реализации входной случайной функции
и выходной случайной функции