Некоторые важные распределения непрерывных случайных величин.
5.1. Равномерное распределение
Закон равной плотности вероятности имеет место, когда все значения непрерывной случайной величины в некотором конечном интервале ( 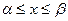 ) равновозможны.
) равновозможны.
Плотность вероятности
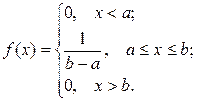
Функция распределения
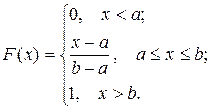
Моменты: 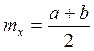 ;
; 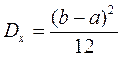 ;
; 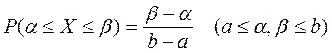 .
.
Показательное (экспоненциальное) распределение
Показательное распределение используется для описания временных интервалов между моментами появления случайных событий в простейшем потоке, подчиняющемся закону Пуассона. Показательное распределениеиграет большую роль в теории случайных процессов.
Плотность вероятности 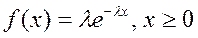 .
.
Функция распределения 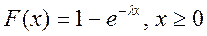 .
.
Моменты: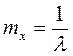 ;
; 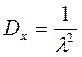 ;
; 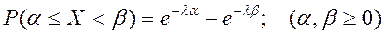 .
.
Значения функции 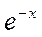 приведены в табл. 5.1.
приведены в табл. 5.1.
Значения функции 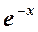 Таблица 5.1.
Таблица 5.1.
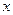
| 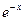
| 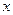
| 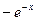
|
| 0,01 0,02 0,05 0,09 0,15 0,2 0,3 0,4 0,5 0,6 0,7 0,8 1,0 | 1,000 0,990 0,980 0,951 0,914 0,861 0,0819 0,741 0,67 0,606 0,549 0,497 0,449 0,368 | 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 6,6 6,7 6,8 7,0 | 0,135 0,082 0,05 0,030 0,0183 0,0111 0,0067 0,0041 0,0025 0,0015 0,0014 0,0012 0,0011 0,0009 |
Нормальное распределение (закон Гаусса)
Нормальное распределение возникает в тех случаях, когда складывается много независимых случайных величин 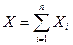 , причем эти величины сравнимы по порядку своего влияния на рассеивание суммы.
, причем эти величины сравнимы по порядку своего влияния на рассеивание суммы.
Плотность вероятности
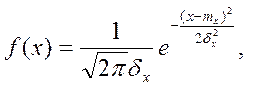
где 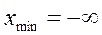 ;
; 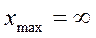 .
.
Дата добавления: 2016-12-09; просмотров: 1752;











