Представление многомерных данных с помощью многомерных матриц. Операции над многомерными матрицами.

Наряду с понятием множества как совокупности неупорядоченных элементов важным понятием является понятие упорядоченного множества элементов. Многомерной матрицей (ММ) называется упорядоченная совокупность многоиндексных элементов ai1i2…iW, где ia = 1,2,…na. Целые положительные числа W, NA = n1n2…nW, na называются соответственно размерностью матрицы А, размером матрицы А, размером индекса ia. Размерность W показывает число индексов в обозначении элементов ai1i2…iW матрицы. Размер NA матрицы А указывает общее число элементов матрицы. Размер индекса na показывает, сколько значений (от 1 до na) пробегает соответствующий индекс.

Структура многомерных матриц определяется структурой их индексов. Структура индекса может быть столбцовой или строчной. Индексы, имеющие, например, строчную структуру (строчные индексы), показывают положение элементов внутри какого-либо столбца. При индексном представлении элементов матрицы целесообразно ставить знак «+» или «–» соответственно над столбцовым или строчным индексом. Например, di+j- - элементы обычной двухмерной (плоской) матрицы. Общее представление многомерной матрицы А имеет вид А = А(p,q), где р – число столбцовых индексов, q – число строчных индексов. Для получения индексного представления многомерной матрицы вводится помечивание индексов. Пометка начинается с последнего индекса, который при q>0 принимается за строчный. Далее столбцовые и строчные индексы чередуются до тех пор, пока один из видов индексов не исчерпывается. При p³q все оставшиеся индексы принимаются за столбцовые, при p<q – за строчные. Числа p и q в сумме дают размерность W матрицы А: p+q = W.

Если матрица А является функциональной, например зависит от времени t, от пространственных координат x, y и т.д., то структурные числа p и q следует отделять от аргументов точкой с запятой, например A = A(p,q;t,x,y). Для наглядного представления многомерной матрицы используют табличное представление. Табличное представление многомерной матрицы – это блочно-иерархическая таблица, отображающая на плоскости структуру матрицы и численные значения элементов. Иерархия согласована с иерархией индексов таким образом, что крайним левым индексам соответствуют наиболее крупные блоки. При этом столбцовые индексы изменяются в столбцах, а строчные – в строках. Примеры представления многомерных матриц приведены в таблице 6.1.

Представление многомерных данных. Таблица 6.1

Общее представление	Индексное представление	Табличное представление
А(0,1)	{ 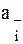-} i =	i=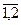1 i=2 a1 a2
А(1,2)	{ 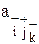}= i, j, k =	i=1 i=1 i=2 i=2   k=1 k=2 k=1 k=2 j=1 a111 a112 a211 a212 j=2 a121 a122 a221 a222

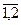
		j = 1	j = 2
B(1,1) = { 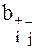} =	i = 1
i, j =	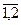i = 2