Функция распределения

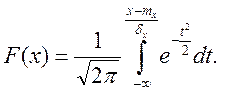
Для вычисления F(x) часто используется табулированная функция

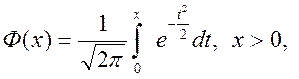
которая называется функцией Лапласа. Функция Лапласа обладает свойствами, которые целесообразно учитывать при расчетах 1) Ф(0) = 0; 2) –Ф(-х) = Ф(х) (нечетная функция); 3) Ф(+¥) = 0,5 и, значит Ф(-¥) = -0,5.

Моменты: ; ; .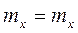

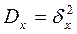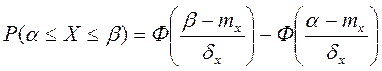Если не принимать во внимание событий, происходящих с веро­ятностями не более 0,0027, то можно практически ограничить диа­пазон возможных значений нормальной случайной величины 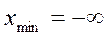; 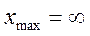. (правило «трех сигма»). Значения функции приведены в табл. 5.2, 5.3.

Значения плотности стандартного нормального распределения 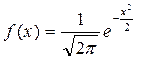. Таблица 5.2.

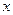
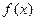
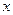
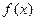
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0	0,3989 0,3970 0,3910 0,3810 0,3683 0,3521 0,3332 0,3123 0,2897 0,2661 0,2420 0,2179 0,1942 0,1714 0,1497 0,1295 0,1109 0,0941 0,0790 0,0656 0,0540	2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0	0,0440 0,0355 0,0283 0,0224 0,0175 0,0136 0,0104 0,0079 0,0060 0,0044 0,0033 0,0024 0,0017 0,0012 0,0009 0,0006 0,0004 0,0003 0,0002 0,0001

Значения функции Лапласа 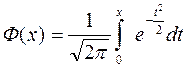. Таблица 5.3

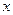
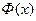
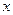
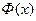
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,5	0,00000 0,03983 0,07926 0,11791 0,15542 0,19146 0,22575 0,25804 0,28814 0,31594 0,34134 0,38493 0,43319	2,0 2,5 2,6 2,7 2,8 2,9 3,0 3,5 4,0 4,5 4,6 4,8 5,0	0,47725 0,49379 0,49534 0,49653 0,49744 0,49813 0,49865 0,49977 0,499968 0,499997 0,49999978 0,49999992 0,49999997

Такое распределение имеет самое важное практическое значение.