Модель межвременного выбора И. Фишера

Ирвинг Фишер (1867-1947) – американский экономист, представитель неоклассического направления в экономической науке. Он разработал модель потребления, учитывающую межвременной выбор. В этой модели предполагает­ся, что:

1) потребитель живет только в двух временных периодах (на­пример, молодость и старость);

2) к концу второго периода потребитель тратит весь накоплен­ный доход (не оставляет после себя никакого наследства);

3) потребитель знает заранее размер своего дохода как в пер­вом периоде (Y₁), так и во втором (Y₂);

4) потребитель может занимать средства или делать сбереже­ния, т.е. потребление в каждом периоде может быть как больше, так и меньше текущего дохода;

5) потребление в обоих периодах является нормальным благом;

6) процентная ставка по займам совпадает с процентной став­кой по сбережениям и является неизменной во времени.

Обозначим потребление в первом периоде С₁, а во втором – C₂, реальную ставку процента r. В первом периоде индивид потребляет С₁, и сберегает (Y₁ – C₁).

Во втором периоде индивид потребляет весь доход второго пе­риода и сбережения первого периода, увеличенные с учетом про­цента на сбережения:

С₂ = Y₂ + (Y₁ – C₁)∙(1 + r). (1.2)

Сбережения (Y₁ – C₁) < 0, если потребитель в первом периоде потребляет больше текущего дохода, занимая под свой доход вто­рого периода. Из (1.2) следует

С₁ + С₂/(1 + r) = Y₁ + Y₂/(1 + r). (1.3)

Соотношение (1.3) показывает, что дисконтированное к пер­вому периоду суммарное потребление равно дисконтированному суммарному доходу. Это ограничение называется межвременным бюджетным ограничением.

По аналогии с теорией поведения потребителя, в которой в ка­честве благ выступает потребление в первом периоде С₁ и во вто­ром периоде С₂, можно считать, что потребитель решает следую­щую задачу:

U(С₁, С₂) → max

при С₁ + С₂/(1 + r) = Y₁ + Y₂/(1 + r). (1.4)

где U(С₁, С₂) – функция полезности потребителя при наборах благ (С₁, С₂).

Из курса микроэкономики известно, что оптималь­ное решение находится в точке касания кривой безразличия и линии бюджетного ограничения (рис. 3.2).

В точке касания А предельная норма замещения потребления первого периода потреблением во втором периоде (MRS) равна отноше­нию цен рассматриваемых благ или тангенсу угла наклона бюд­жетного ограничения: MRS = 1 + r.

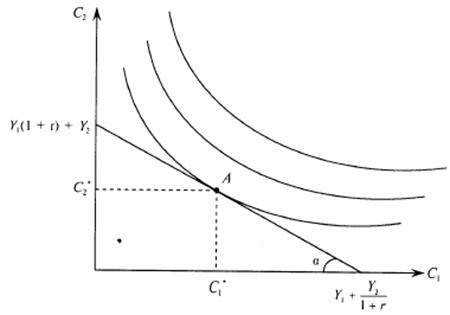
Рисунок 1.3 – Оптимальное решение потребителя в модели межвременного выбора

Увеличение дохода в любом периоде (при прочих равных усло­виях) увеличивает дисконтированный суммарный доход и, следова­тельно, на графике сдвигает линию бюджетного ограничения па­раллельно вправо. Так как потребление является нормальным бла­гом, то его величина в обоих периодах увеличивается (рис. 1.4). Новой оптимальной точкой становится точка В: С₁^** > С₁^*; С₂^** > С₂^*.

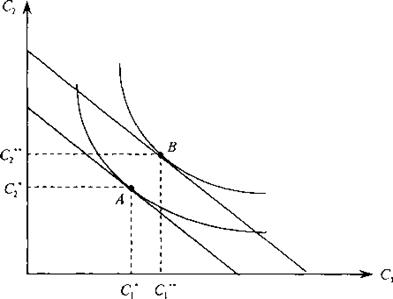
Рисунок 1.4 – Изменение оптимального решения потребителя при росте дохода

в одном из периодов

Это означает, что потребление в первом периоде возрастает, если в будущем ожидается увеличение дохода, даже при неизмен­ном текущем доходе. Функция потребления Кейнса такой воз­можности не учитывает.

Увеличение ставки процента приводит к тому, что меняется соотношение цен потребления в первый и второй период. На (рафике линия бюджетного ограничения становится круче. По­требитель может теперь больше, чем раньше, потребить в буду­щем, отказываясь от единицы потребления в настоящем. Таким образом, при росте ставки процента растет альтернативная стои­мость (относительная цена) потребления в первом периоде. Поэтому в соответствии с эффектом замещения увеличится потреб­ление во второй период и уменьшится в первый. Заметим, что точка, отражающая решение потребителя потребить весь доход первого периода в первом периоде, а весь доход второго – во втором (С₁ = Y₁; С₂ = Y₂), лежит на линии бюджетного ограниче­ния. При росте ставки процента новая линия бюджетного ограни­чения будет по-прежнему проходить через эту точку.

В модели рассматриваются потребители двух типов:

1) те, кто предпочитает сберечь часть дохода первого периода, чтобы больше потратить во втором, – кредиторы, или сбе­регатели;

2) те, кто предпочитает занять под доход второго периода, что­бы больше потратить в первом, – заемщики.

При росте ставки процента сберегатель получает больший до­ход на сбережения первого периода, поэтому его доход во втором периоде возрастает, и он сможет потребить больше, чем раньше в обоих периодах (эффект дохода). Таким образом, сберегатель будет потреблять во втором периоде больше, чем раньше (эффект дохода и эффект замены действуют в одном направлении). По­требление первого периода может как увеличиться (эффект дохо­да окажет большее влияние, чем эффект замещения; см. рис. 1.5), так и уменьшиться (эффект замещения перекроет эффект дохода). Конкретный результат зависит от предпочтений, отражаемых конкретной функцией полезности.

С помощью аналогичных рассуждений легко показать, что для заемщика увеличение ставки процента уменьшит потребление в первом периоде и может как увеличить, так и уменьшить потребление во втором периоде.

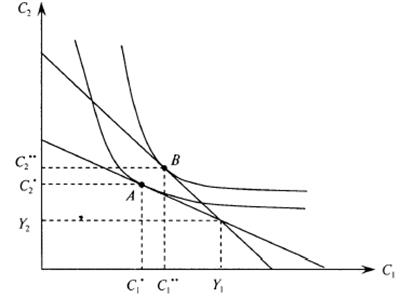
Рисунок 1.5 – Изменение решения сберегателя при росте ставки процента

Если в экономике слабо развит кредитный рынок, т.е. существуют ограничения по заимствованию, то заемщики не всегда могут потреблять в текущем периоде величину, бóльшую текущего дохода. В этом случае потребители решают оптимизационную задачу (1.4) при .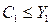

Бюджетное ограничение примет вид ломаной линии (см. рис. 1.6). Для сберегателя решение останется таким же, как в стандартном варианте. Для заемщика наилучшим окажется угловое решение (точка А), при котором С₁ = Y₁, С₂ = Y₂. Это означает, что при су­ществовании ограничений по заимствованию часть потребителей основывает свои решения только на текущем доходе.

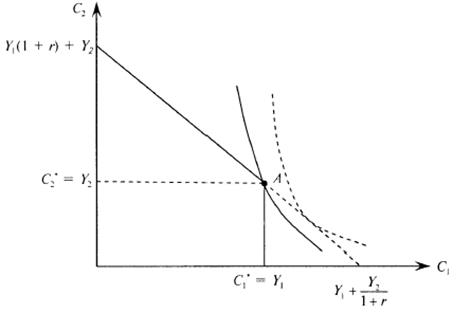
Рисунок 1.6 – Решение заемщика при ограничении по заимствованию

Основной заслугой модели Фишера является выявление меж­временного характера потребительских решений. Эти идеи по­служили отправной точкой теорий потребления, предложенных Ф.Модильяни и М.Фридманом, а также всех их современных мо­дификаций.