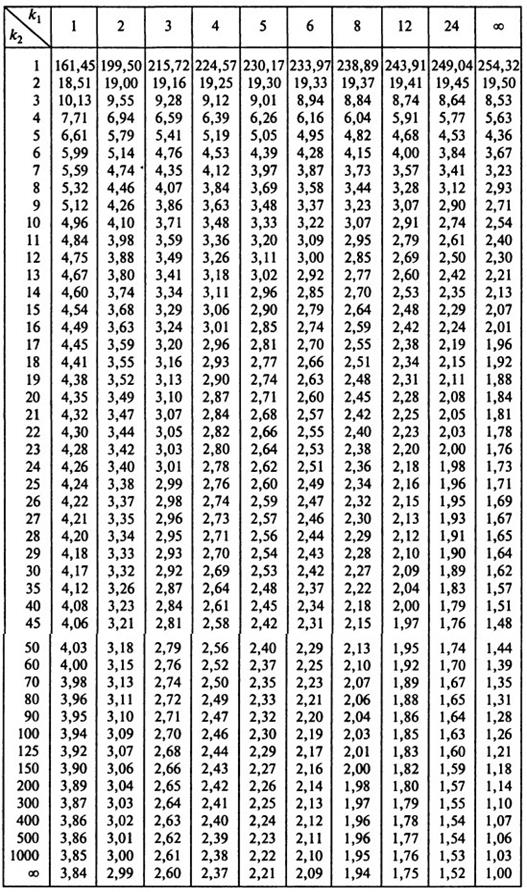
Приложение А. Значения статистики критерия Фишера


Приложение Б. Значения статистики критерия Стьюдента

k Уровень значимости α (двусторонняя критическая область)
0,1 0,05 0,02 0,01 0,001
6,3138 12,7062 31,8205 63,6567 636,6192
2,0150 2,5706 3,3649 4,0321 6,8688
1,9432 2,4469 3,1427 3,7074 5,9588
1,8946 2,3646 2,9980 3,4995 5,4079
1,8595 2,3060 2,8965 3,3554 5,0413
1,8331 2,2622 2,8214 3,2498 4,7809
1,8125 2,2281 2,7638 3,1693 4,5869
1,7959 2,2010 2,7181 3,1058 4,4370
1,7823 2,1788 2,6810 3,0545 4,3178
1,7709 2,1604 2,6503 3,0123 4,2208
1,7613 2,1448 2,6245 2,9768 4,1405
1,7531 2,1314 2,6025 2,9467 4,0728
1,7459 2,1199 2,5835 2,9208 4,0150
1,7396 2,1098 2,5669 2,8982 3,9651
1,7341 2,1009 2,5524 2,8784 3,9216
1,7291 2,0930 2,5395 2,8609 3,8834
1,7247 2,0860 2,5280 2,8453 3,8495
1,7207 2,0796 2,5176 2,8314 3,8193
1,7171 2,0739 2,5083 2,8188 3,7921
1,7139 2,0687 2,4999 2,8073 3,7676
1,7109 2,0639 2,4922 2,7969 3,7454
1,7081 2,0595 2,4851 2,7874 3,7251
1,7056 2,0555 2,4786 2,7787 3,7066
1,7033 2,0518 2,4727 2,7707 3,6896
1,7011 2,0484 2,4671 2,7633 3,6739
1,6991 2,0452 2,4620 2,7564 3,6594
1,6973 2,0423 2,4573 2,7500 3,6460
1,6839 2,0211 2,4233 2,7045 3,5510
1,6759 2,0086 2,4033 2,6778 3,4960
1,6669 1,9944 2,3808 2,6479 3,4350
1,6620 1,9867 2,3685 2,6316 3,4019
1,6602 1,9840 2,3642 2,6259 3,3905
∞ 1,6448 1,9600 2,3263 2,5758 3,2905
  0,05 0,025 0,01 0,005 0,0005
Уровень значимости α (односторонняя критическая область)

Приложение В. Значения статистики критерия Дарбина-Уотсона

Таблица П.В.1.Значения статистик dL и dU критерия Дарбина –Уотсона при уровне значимости a = 0,05

( n-число наблюдений, p- число объясняющих переменных).

 

n p=1 dL dU p=2 dL dU p=3 dL dU p=4 dL dU
1.08 1.36 0.95 1.54 0.82 1.75 0.69 1.97
1.10 1.37 0.98 1.54 0.86 1.73 0.74 1.93
1.13 1.38 1.02 1.54 0.90 1.71 1.78 1.90
1.16 1.39 1.05 1.53 0.93 1.69 1.82 1.87
1.18 1.40 1.08 1.53 0.97 1.68 0.85 1.85
1.20 1.41 1.10 1.54 1.00 1.68 0.90 1.83
1.22 1.42 1.13 1.54 1.03 1.67 0.93 1.81
1.24 1.43 1.15 1.54 1.05 1.66 0.96 1.80
1.26 1.44 1.17 1.54 1.08 1.66 0.99 1.79
1.27 1.45 1.19 1.55 1.10 1.66 1.01 1.78
1.29 1.45 1.21 1.55 1.12 1.66 1.04 1.77
1.30 1.46 1.22 1.55 1.14 1.65 1.06 1.76
1.32 1.47 1.24 1.56 1.16 1.65 1.08 1.76
1.33 1.48 1.26 1.56 1.18 1.65 1.10 1.75
1.34 1.48 1.27 1.56 1.20 1.65 1.12 1.74
1.35 1.49 1.28 1.57 1.21 1.65 1.14 1.74
1.36 1.50 1.30 1.57 1.23 1.65 1.16 1.74
1.37 1.50 1.31 1.57 1.34 1.65 1.18 1.73
1.38 1.51 1.32 1.58 1.26 1.65 1.19 1.73
1.39 1.51 1.33 1.58 1.27 1.65 1.21 1.73
1.40 1.52 1.34 1.58 1.28 1.65 1.22 1.73
1.41 1.52 1.35 1.59 1.29 1.65 1.24 1.73

Таблица П.В.2Значения статистик dL и dU критерия Дарбина –Уотсона

при уровне значимости a = 0,01

( n-число наблюдений, p- число объясняющих переменных)

 

n p=1 dL dU p=2 dL dU p=3 dL dU p=4 dL dU
0,81 1,07 0,70 1,25 0,59 1,46 0,49 1,70
0,84 1,09 0,74 1,25 0,63 1,44 0,534 1,66
0,87 1,10 0,77 1,25 0,67 1,43 0,57 1,63
0,90 1,12 0,80 1,26 0,71 1,42 0,61 1,60
0,93 1,13 0,83 1,26 0,74 1,41 0,65 1,58
0,95 1,15 0,86 1,27 0,77 1,41 0,68 1,57
0,97 1,16 0,89 1,27 0,80 1,41 0,72 1,55
1,00 1,17 0,91 1,28 0,83 1,40 0,75 1,54
1,02 1,19 0,94 1,29 0,86 1,40 0,77 1,53
1,04 1,20 0,96 1,30 0,88 1,41 0,80 1,53
1,05 1,21 0,98 1,30 0,90 1,41 0,83 1,52
1,07 1,22 1,00 1,31 0,93 1,41 0,85 1,52
1,09 1,23 1,02 1,32 0,95 1,41 0,88 1,51
1,10 1,24 1,04 1,32 0,95 1,41 0,90 1,51
1,12 1,25 1,05 1,33 0,99 1,42 0,92 1,51
1,13 1,26 1,07 1,34 1,01 1,42 0,94 1,51
1,15 1,27 1,08 1,34 1,02 1,42 0,96 1,51
1,16 1,28 1,10 1,35 1,04 1,43 0,98 1,51
1,17 1,29 1,11 1,36 1,05 1,43 1,00 1,51
1,18 1,30 1,13 1,36 1,07 1,43 1,01 1,51
1,19 1,31 1,14 1,37 1,08 1,44 1,03 1,51
1,21 1,32 1,15 1,38 1,10 1,44 1,04 1,51

Приложение Г. Исследование уравнений регрессии

С помощью пакетов прикладных программ Excel

Общие сведения

Исследование линейного уравнение регрессии с помощью ППП Excel возможно с использованием встроенной статистической функции ЛИНЕЙН, либо с помощью инструмента анализа данных РЕГРЕССИЯ. Рассмотрим каждый из этих вариантов [18, 21, 29].

1. Встроенная статистическая функция ЛИНЕЙН определяет параметры a,b линейного уравнения регрессии y=a+b∙x. Порядок вычислений следующий:

1.1. Введите исходные данные или откройте существующий файл, содержащий анализируемые данные.

1.2. Выделите область пустых ячеек 5×2 (5 строк и 2 столбца) для вывода результатов регрессионной статистики (или область 1×2 –для получения только оценок коэффициентов регрессии).

1.3. Активизируйте Мастер функций, в окне Категория выберите Статистические, в окне Функция – Линейн.

1.4. Заполните аргументы функции:

Известные значения y - диапазон, содержащий данные зависимой переменной Y;

Известные значения x - диапазон, содержащий данные независимой переменной X;

Константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении регрессии. Если Константа=1, то свободный член a в уравнении регрессии рассчитывается обычным образом; если Константа=0, то свободный член равен нулю, a =0.

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика=1, то выводится дополнительная информация; если Статистика=0, то выводятся только оценки параметров уравнения.

1.5. После заполнения аргументов в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нужно нажать на клавишу «F2», а затем на комбинацию клавиш «CTRL»+«SHIFT»+«ENTER». Дополнительная регрессионная статистика будет выводиться в следующем порядке:

 

Значение коэффициента b Значение коэффициента a
Среднее квадратическое отклонение параметра b Среднее квадратическое отклонение параметра a
Коэффициент детерминации R2 Среднее квадратическое отклонение y (σост)
F-статистика Число степеней свободы (n-m)
Факторная сумма квадратов (RSS) Остаточная сумма квадратов (ESS)

 

2. С помощью инструмента анализа данных Регрессия,помимо результатов регрессионной статистики, можно выполнить дисперсионный анализ, построить доверительные интервалы для параметров уравнения регрессии, можно получить остатки, графики остатков и графики подбора линии регрессии. Последовательность подключения и работы с инструментом анализа данных следующая:

2.1. Для подключения пакета анализа данных в главном меню последовательно выберите Сервис/Надстройки. Установите флажок у надстройки Пакет анализа.

2.2 В главном меню выберите Сервис/Анализ данных/Регрессия.

2.3. Заполните диалоговое окно ввода данных и параметров вывода.

Выходной интервал Y - здесь требуется задать состоящий из одного столбца диапазон анализируемых зависимых данных.

Входной интервал Х - здесь требуется задать диапазон значений независимой переменной (или нескольких независимых переменных).

Метки — здесь требуется установка флажка, если первая строка или первый столбец входного интервала содержит заголовки. Если заголовков нет, то флажок надо снять. Для удобства последующего анализа полученных результатов рекомендуется всегда иметь заголовочную строку (или столбец) в поле исходных данных и поэтому всегда включать метки во входной интервал (не забывать щелкать по флажку "метки"). Если мы забудем включить этот флажок при наличии меток, то вместо расчета получим прерывание и сообщение "Входной интервал содержит нечисловые данные".

Уровень надежности - по умолчанию, применяется уровень 95%. Установить флажок, если нужно включить в выходной диапазон дополнительный уровень, а в поле (рядом) ввести уровень надежности, который будет использован дополнительно к применяемому.

Константа – ноль – этот флажок необходимо пометить только в том случае, если нужно получить уравнение без свободного члена, чтобы линия регрессии прошла через начало координат.В целях исключения ошибок спецификациимодели линейной регрессиирекомендуется не активизировать этот флажок и всегда рассчитывать значение константы; в дальнейшем, если это значение окажется незначимым, им можно пренебречь.

Выходной диапазон - здесь требуется определить левую верхнюю ячейку выходного диапазона. Необходимо минимум семь столбцов для итогового диапазона, который будет включать в себя: результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов. В случае сложной задачи, где требуется получить большое число результатов исследования уравнений, лучше воспользоваться возможностью размещения каждого из них на новом рабочем листе.

Новый лист - здесь требуется установить переключатель для открытия нового листа в книге под результаты анализа, начиная с ячейки А1. Можно ввести имя нового листа в поле напротив переключателя.

Остатки- установкой этого флажка заказывается включение остатков в выходной диапазон. Для получения максимума информации в ходе исследования рекомендуется активизировать этот и все описанные ниже флажки диалогового окна.

График остатков - чтобы построить диаграмму остатков для каждой независимой переменной, нужно установить этот флажок.

График подбора - это важнейший график, а точнее серия графиков, показывающих насколько хорошо теоретическая линия регрессии (т.е. предсказания) подобрана к наблюдаемым данным.

 


Дата добавления: 2018-05-10; просмотров: 3759;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.017 сек.