Задачи для практических занятий и самостоятельной работы

1. Построить графически с помощью таблиц законы распределения (ряды, плотности вероятностей, функции распределения) случайных величин.

Открыть приложение MS Excel.

В первой строке записать число успехов опыта. Например, от 0 до 5 (рис.4.2).

Во второй строке - биномиальный закон распределения. Для этого необходимо поставить курсор в ячейку, стоящую ниже числа успехов (b2) и вызвать статистическую функцию БИНОМРАСП. Ввести следующие аргументы:

- число s: номер ячейки со случайной величиной (b1);

- испытания: число испытаний (5);

- вероятность: любое число от 0 до 1 (0,5);

- интегральный: логическое значение, определяющее вид функции; интегральная функция распределения (ЛОЖЬ) (вторая строка) или функция плотности распределения (ИСТИНА). (третья строка)

в четвертой строке – геометрический ряд распределения, описываемый формулой 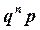. (Этот закон не указан в списке стандартных функций Excel, поэтому его нужно задавать пользователю по формуле). Функция СТЕПЕНЬ (p; n)*q, где p – вероятность (в нашем случае – 0,6), n – номер ячейки (b1), q=1- p (в нашем случае – 0,4);

в пятой строке – гипергеометрический ряд распределения, предусматривающий функцию ГИПЕРГЕОМЕТ (количество успешных испытаний в выборке; размер выборки; количество успешных испытаний в генеральной совокупности; размер генеральной совокупности). В нашем случае формула выглядит так: ГИПЕРГЕОМЕТ (b1;5;5;100);

в шестой строке – ряд распределения Пуассона (функция плотности распределения) ПУАССОН (количество событий; среднее; интегральный) в нашем случае ПУАССОН(b1;1,6;ложь);

в седьмой строке – ряд распределения Пуассона (интегральная функция распределения) ПУАССОН (b1; 1,6; истина).

Для того, чтобы графически отобразить интегральный закон распределения (функцию распределения), необходимо сначала вычислить его аналитически вместо ряда распределения. Ввести матрицу А (n´n), где n – число успехов опыта (в примере – 6). Матрица изображена на листе Excel в диапазоне (A10:F15). В диапазоне (H10:H15) – транспонированная матрица ряда геометрического распределения. Для умножения матриц используем функцию МУМНОЖ (массив 1; массив 2). В нашем случае - МУМНОЖ (A10:F15;H10:H15) в ячейке I10. Результирующая матрица получается так – выделим место под нее, активизируем строку формул и нажмем комбинацию клавиш Ctrl+Shift+Enter.

Для геометрического закона построить функцию распределения и плотность распределения.

То же самое проделать для гипергеометрического распределения и для распределения Пуассона.

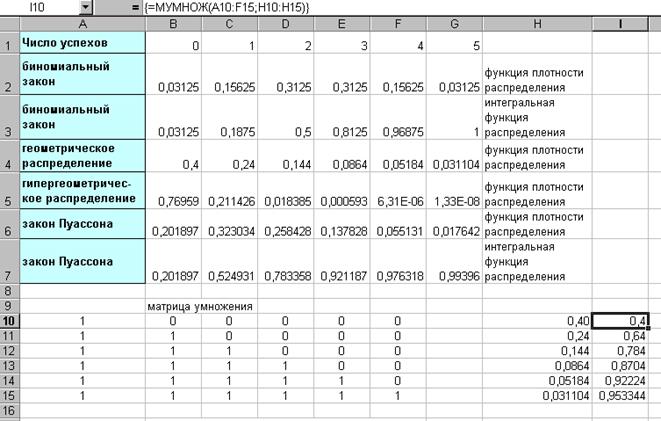
Рис. 4.2. Изучение законов распределения дискретных случайных величин

2. Отметить значения, соответствующие математическому ожиданию, моде, медиане и отклонениям от математического ожидания.

3. Найти вероятность попадания значения СВ в заданный интервал.

Тема №5.