Определение достоверности уравнения множественной линейной регрессии по критерию Фишера, коэффициенту множественной корреляции.
Для оценки достоверности модели применяется критерий Фишера и коэффициент множественной корреляции.
Критерий Фишера:
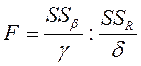 ,
,
где γ=n – число факторов (C1 и C2),
δ=G-n-1, G – число экспериментов (в данном примере 10),
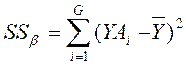 - разброс линии регрессии вокруг среднего значения данных,
- разброс линии регрессии вокруг среднего значения данных,
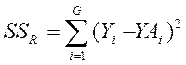 - разброс данных вокруг линии.
- разброс данных вокруг линии.
Если Yi =YA i, то R→ ∞.
Далее в Microsoft Excel заполняется следующая таблица:
| A | B |
| =1-FРасп(А1; n числ; n знам) | |
| ... | |
И по полученным значениям строится график, по которому находится значение F критическое.
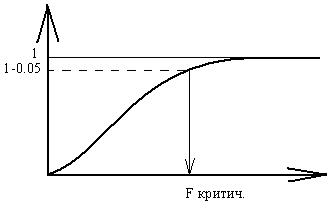
Рис. 9.1. Определение значения Fкритич.
С заданной погрешностью, равной 5%, находится значение F критическое.
Если F > F критич, то модель принимается.
Коэффициент множественной корреляции:
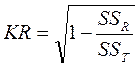 ,
,
где 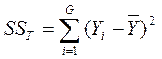 - разброс данных вокруг их среднего значения,
- разброс данных вокруг их среднего значения,
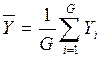 - среднее значение.
- среднее значение.
Если Yi =YA i, то 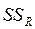 = 0 и KR =1 – точное полное отображение процесса.
= 0 и KR =1 – точное полное отображение процесса.
Пример. Задана таблица роста и веса 9 девушек.
| Рост, x | |||||||||
| Вес, y |
Составим уравнение регрессии Y=C0 + C1*X1. В программе MS Excel найдем коэффициенты Ci.
C0 = 13,37, C1 = 0,31, т.е. уравнение регрессии имеет вид y = 13,37 + 0,31*x1.
Дата добавления: 2016-12-09; просмотров: 2268;











