Чётность и нечётность.

Чётная функция: 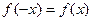. График чётной функции симметричен относительно оси 0y, т.е. при зеркальном отражении переходит в точно такой же график, примером может быть парабола, а также cos(x).

Нечётная функция: 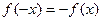. График нечётной функции симметричен относительно точки (0,0), то есть после поворота на 180⁰ график был бы таким же, примером может быть кубическая парабола или любая другая нечётной степени, или например синус, тангенс.

Существует такое неочевидное свойство разложения на чётные и нечётные компоненты:

Свойство. Любая функция f представима в виде суммы чётной и нечётной, то есть .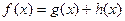

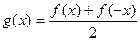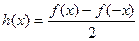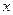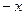Доказательство.Введём две функции: , . Первая из них чётна, вторая нечётна. Видно, что если заменить на , то для 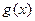получится выражение, равное исходному, а вот для 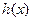разность в числителе будет противоположна: = .

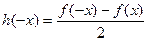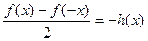Сумма этих функций: = = = .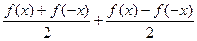

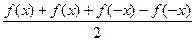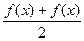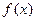итак, .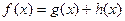

Если чётную и нечётную компоненты записать для функции 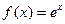, то получатся так называемые гиперболический косинус и гиперболический синус: , .

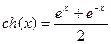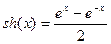Вообще, существует 3 способа задания функций - явный, неявный, параметрический.

Способ задания:	Явно	Неявно	Параметрически
Вид уравнения: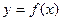
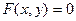
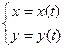
Пример (окружность)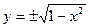
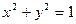
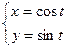
Пример (прямая)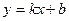

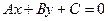
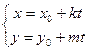
Для поверхностей тоже существуют эти 3 способа:

Явный: Неявный: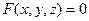

Параметрический: 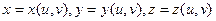(в этом случае обязательно будет два параметра). Например, 2 параметра на сфере: широта и долгота.

Пределы.