Свойства эквивалентных бесконечно малых.
1. Если 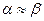 , то
, то 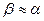 .
.
Доказательство очевидно, 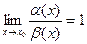 то
то 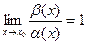
2. Если 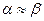 и
и 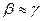 то
то 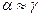 .
.
Дано: 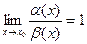 ,
, 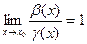 . Докажем, что
. Докажем, что 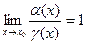 .
.
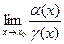 =
= 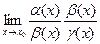 =
= 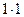 = 1.
= 1.
3. Порядок разности двух эквивалентных величин больше, чем порядок малости каждой из них.
Доказательство. Дано: 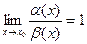 . Докажем, что при делении разности на любую из них предел будет 0, это как раз и означает, что в числителе - более высокого порядка.
. Докажем, что при делении разности на любую из них предел будет 0, это как раз и означает, что в числителе - более высокого порядка.
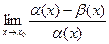 =
= 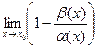 = 1-1 = 0.
= 1-1 = 0.
4. Порядок малости суммы равен наименьшему из порядков слагаемых.
Доказательство. Пронумеруем так, чтобы 1-е слагаемое было наименьшего порядка. Тогда: 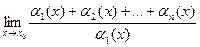 =
= 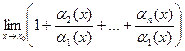 = 1+0+...+0 = 1.
= 1+0+...+0 = 1.
То есть, эта сумма эквивалентна слагаемому наименьшего порядка.
Пример: 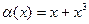 1-го а не 3-го порядка малости в точке x = 0.
1-го а не 3-го порядка малости в точке x = 0.
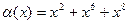 - 2-го порядка.
- 2-го порядка.
А вот если рассматривать предел при 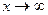 , то тогда 8-го порядка. При малых значениях наибольшее влияние на сумму оказывает наименьшая степень, а при бесконечном возрастании - наибольшая степень.
, то тогда 8-го порядка. При малых значениях наибольшее влияние на сумму оказывает наименьшая степень, а при бесконечном возрастании - наибольшая степень.
4а. Порядок суммы бесконечно-больших равен наибольшему из порядков слагаемых.
5. Если 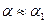 ,
, 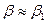 и
и 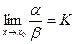 то
то 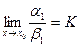
то есть этот предел тоже существует, и равен К.
Доказательство. Дано: 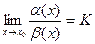 ,
, 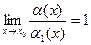 ,
, 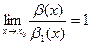 .
.
Вычислим 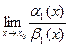 =
= 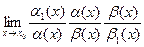 =
= 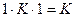 .
.
Это свойство даёт возможность в дробях фактически заменять более сложные бесконено-малые на более простые, как правило, даже на степенные.
Пример. 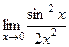 =
= 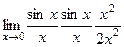 =
= 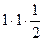 =
= 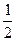 .
.
Домножили и поделили, так что первая дробь стала состоять из двух эквивалентных величин, и её предел равен 1. А выглядит это так, как будто в числителе просто заменили 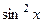 на эквивалентную
на эквивалентную 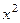 .
.
Лекция № 11. 18. 11. 2016
Дата добавления: 2016-11-29; просмотров: 1687;











