Внутренние и граничные точки.

Если для точки 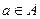существует окрестность, которая полностью лежит во множестве А, то есть является его подмножеством, 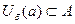, то такая точка называется внутренней точкой множества А. Если же для любой окрестности есть лишь частичное пересечение со множеством А, то такая точка называется граничной точкой множества. Показано на чертеже:

Функция, аргумент, образ.

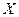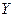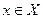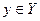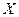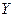Пусть даны 2 множества , . Если задан некоторый способ каждому элементу поставить в соответствие какой-то , то говорится, что задана ФУНКЦИЯ из в . Обозначение: .

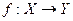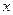называется аргументом функции, а 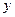- образом.

Основные элементарные функции и их графики: повторить из школьного курса (!)

Степенные 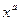, показательные 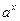, логарифмические 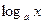, тригонометрические 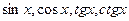, обратные тригонометрические.

Лекция № 9. 28. 10. 2016

Если 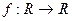, то есть 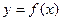, график - кривая в плоскости.

Если функция двух переменных, то есть , её график - это поверхность в трёхмерном пространстве.

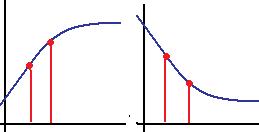
Монотонность.

Монотонно возрастающая функция: если 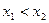то .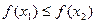

Монотонно убывающая функция: если 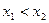то .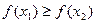

Периодичность.

Если существует такое числ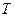о , что верно 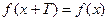то функция называется периодической, 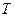- период.

Примеры. , 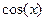период 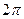, , 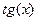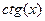период .

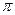О влиянии коэффициента на период. Если 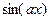период равен 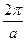. Если 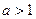, колебания становятся чаще, а период меньше. Почему так происходит? Точка 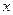прошла расстояние 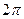, в это время - прошло в 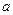раз больше, то есть в 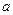раз больше колебаний произошло на этом отрезке, длина которого 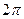. Если 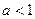наоборот, период больше, а колебания реже, чем у исходного графика.