Последовательность.

Множество чисел, пронумерованных с помощью натуральных чисел: 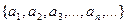называется последовательностью. Её можно определить также и как функцию .

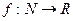Графиком будет не кривая, а дискретный набор точек, потому что только над каждой точкой с абсциссой, равной натуральному числу, есть точка графика.

Например, 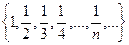- последовательность.

Арифметическая и геометрическая прогрессии тоже частный случай последовательности.

Пример: 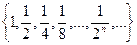геометрическая прогрессия

В рассмотренных примерах видно, что при возрастании номера элемент убывает к 0. Однако при этом само число 0 не достигается ни при каком номере. То есть, числа 0 в этой последовательности нет. Однако, все элементы уменьшаются и приближаются к 0. В связи с этим возникает определение предела последовательности:

Определение. Число 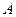называется пределом последовательности 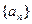, если: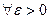 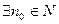, такое, что 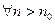выполняется: .

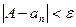(для любого числа эпсилон больше нуля, существует такой номер элемента последовательности, что для всех последующих номеров отклонение элементов от числа А меньше, чем эпсилон). В этом случае говорится, что последовательность стремится к числу А.

Обозначение предела: 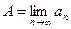. (lim это от английского слова limit которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).

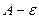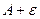Если рассмотреть полосу от до по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:

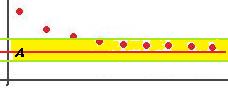
Чем меньше число 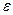(погрешность меньше) тем больший номер требуется .

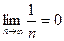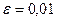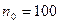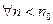Пример. . По определению: если например требуемая точность то , выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.

* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например 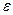= 10 км.) существует такой момент времени 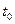, что в последующие моменты времени 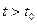расстояние будет меньше, чем 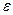. Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать 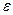= 5 км. то это достигается в более поздний момент времени, а если 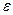= 1 км. то ещё позже.

Предел может и не существовать. Для последовательности 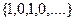, например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа .

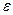Рассмотрим последовательность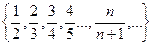

Вычислим предел. 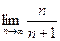= = 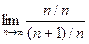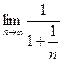. Второе слагаемое в знаменателе стремится к 0. В итоге, 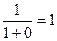, 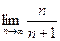=1.

Таким же методом можно сокращать старшие степени и в других случаях, для произвольных степеней.

= = .

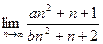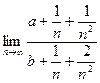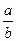В общем случае, когда степени разные: = .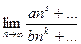

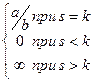Пример. Вычислить предел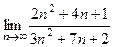

Решение.Здесь неопределённость типа 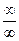. Сократим на :

= = .

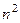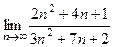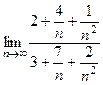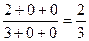Пример. Вычислить предел .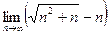

Комментарий. В выражениях с неопределённостью типа 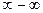ответ не виден из самого выражения. Так, если 2 объекта от нас удаляются в бесконечность, то при этом расстояние между ними может уменьшаться, может стабилизироваться на каком-то уровне, а может возрастать. Например, для 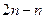оба слагаемых стремятся к бесконечности, но и разность между ними тоже увеличивается неограниченно. А в разности 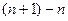оба слагаемых увеличиваются, но разность стабильна и равна 1. Поэтому при решении таких примеров снаала нужны преобразования, приводящие к виду дроби, а там уже можно сократить на какой-то множитель.

Итак, 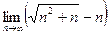умножим на сопряжённое выражение, то есть на сумму, подобную этой разности. Тогда можно будет применить формулу сокращённого умножения, и корень исчезнет, так как он будет возведён в квадрат.

= = = =

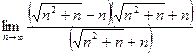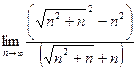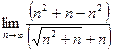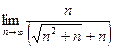
В знаменателе содержится n и выражение, содержащее корень из 2 степени, которое по скорости роста сопоставимо с n. Сократим числитель и знаменатель на n.

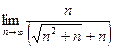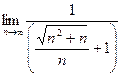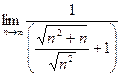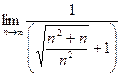= = = . Чтобы разделить корень, удобно факт деления на n представили как деление на корень из n², продолжим:

= = .

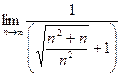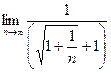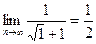Вычислительный эксперимент. Чтобы луше понять понятие предела, можете вычислить выражение 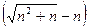например, при n = 100, n = 1000 на калькуляторе. Чем больше n тем ближе к 0,5 ответ получится.

n = 100 результат 0,49876. Отклонение от 1/2 составило 0,00124.

n = 1000 результат 0,49988. Отклонение от 1/2 составило 0,00012.

Теорема 1. Пусть дано 3 последовательности, причём для любого номера n: 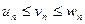. Если , .

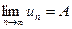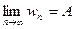
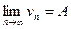Доказательство. Так как для первой и третьей последовательности предел равен А, то числа 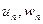(начиная с какого-то номера) отклоняются от 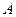не больше чем на величину 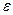, то есть принадлежат интервалу 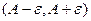. Но число 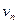находится между ними, тогда оно тоже принадлежит 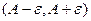. Тогда по определению, для средней последовательности тоже существует предел.

Теорема 2. Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.

Примеры нарушения одного из этих двух условий.

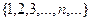не ограничена, предел .

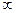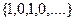не монотонна. Пределом не может быть ни одно из чисел 0 или 1. Здесь после любого элемента, среди последующих есть какой-либо, удалённый от данного на расстояние 1, то есть в определении предела было бы не «для любого 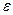», а только для 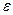>1. Колебания по высоте не уменьшаются, все последующие элементы не впишутся в узкую полосу ширины .

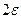Предел функции при .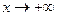

Число 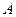называется пределом функци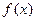и , пр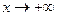и если:

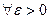
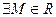, так, что 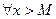выполняется: .

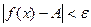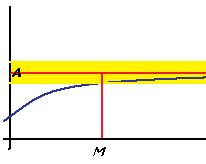
Объяснение: для любой заранее заданной погрешности 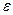существует такая константа М, что правее неё график отклоняется от ординаты А не более, чем на .

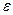Аналогично определяется предел при 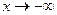для левой полуоси.

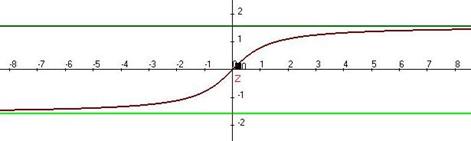
Пример. 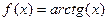. Два различных предела при 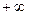и 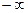. . 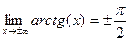Предел на правой полуоси равен 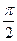, но при этом ни в одной точке 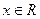функция не принимает это значение.

Пример. Найти 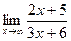.Вычисление проводится таким же методом, как в случае последовательности, где было 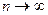. Сократим на 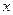, получим = .

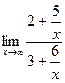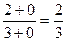Как видим, вычислять пределы для дробно-рациональных выражений можно тем же методом, что было для последовательностей. Как видим, эта ситуация сильно напоминает то, что было в случае пределов последовательностей, только там дискретная величина 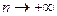а здесь непрерывная, .

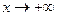Предел функции в точке (при ).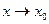

Определение. Число 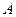называется пределом функции 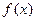в точке 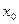, если: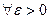 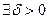, такое, что при 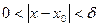выполняется: .

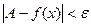(для любого числа эпсилон больше нуля, существует такое число дельта, так что если модуль разности 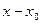меньше дельта, то модуль разности 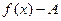меньше, чем эпсилон).

Обозначение .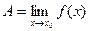

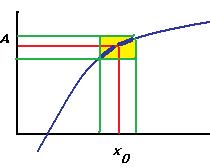
В случае существования предела, получается, что задавая погрешность 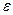можно найти такой интервал в области определения, что отклонение значений от А будет меньше чем 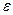. Фактически, часть графика впишется в некоторый прямоугольник, при уменьшении одной стороны будет уменьшаться и вторая.

У студентов может закономерно возникнуть вопрос, а для чего вообще нужно понятие предела в точке, и почему нельзя просто подставить 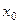и вычислить функцию. Проблема в том, что не всегда значение функции существует в точке. Иногда бывает так, что формально её вычислить нельзя. Например, для функции 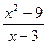значение в точке 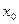=3 не существует. При вычислении на калькуляторе поочерёдно числителя и знаменателя, получили бы 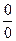и калькуляторы, компьютеры выдали бы сообщение об ошибке. Но ведь в соседних точках значение функции есть. График функции подходит к некоторой точке в плоскости. Так вот, её ордината и равна этому пределу.

Пример. Вычислить предел .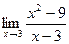

В точке 3 значение функции не существует, однако во всех соседних точках существует, и можно узнать, к какой ординате стремится график при 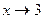. Разложим на множители:

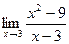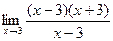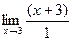= = = 6.

Тот множитель, который отвечал за стремление к 0 в числителе и знаменателе, сокращён, поэтому далее удалось просто подставить 3 и получить ответ.

Как видим, методы разные: если неопределённость типа 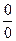, то выделяем множители, чтобы сократить те множители, которые стремятся к 0. Если неопределённость 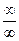, то корни искать не нужно, а нужно сократить на степенную функцию старшей степени. Для неопределённостей типа 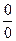основным методом является разложение на множители, и сокращение тех множителей, которые ответственны за стремление к 0.

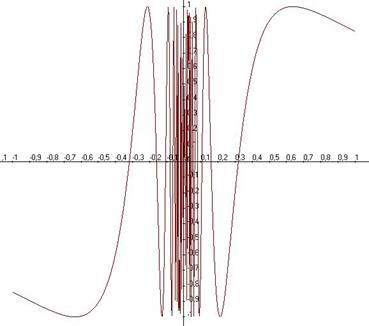
Пример функции, не имеющей предела в нуле. 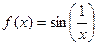. Здесь при приближении к 0 бесконечное число колебаний, то есть, уменьшая область определения, например интервал 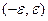, никак не удастся получить уменьшение области значений функции над этим интервалом, размах колебаний всё равно останется от -1 до 1. При подходе абсциссы к 0, функция здесь должна пройти бесконечное число колебаний амплитуды 2 (от -1 до 1).

Лекция № 10. 11. 11. 2016

Метод Лопиталя для неопределённостей 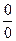. Несмотря на то, что тема «производные» подробно будет позже, и доказательство этого метода будет дано в той теме, производные для некоторых элементарных функций известны из школы, и можно этим пользоваться при вычислении пределов.

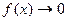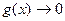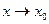Если , при и ,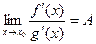

то .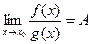

Пример. = = = .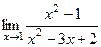

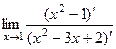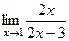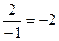Этот метод можно применять и в 2 или более шагов, если после 1-го дифференцирования остаётся неопределённость .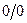

Вычислим этим же способом 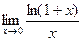= = 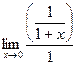1.

График ln(1+x) это ln(x) сдвинутый влево на 1, касательная проходит ровно под углом 45 градусов, то есть совпадает с функцияей y = x. Если рассмотреть при большом увеличении, они почти неотличимы.

Ещё пример. .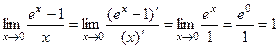

Ещё пример. .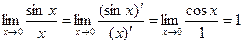

1-й замечательный предел. .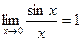

Доказательство 1-го замечательного предела из геометрических соображений.

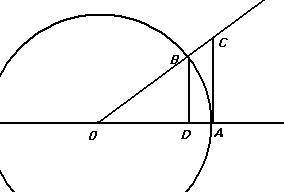
Рассмотрим единичную окружность, и какой-либо угол. Длина дуги AB равна 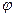- это по определению радианной меры угла. Так как ОА это радиус, а мы взяли единичную окружность, то

.

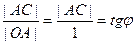Так как ОВ это тоже радиус, то .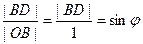

Но длина дуги на чертеже больше, чем отрезок BD, и меньше, чем AC.

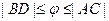, то есть .

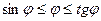Совпадают они именно при .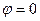

Кстати, графики трёх функций именно так и расположены: у них общая касательная, тангенс выше, синус ниже, чем биссектриса.

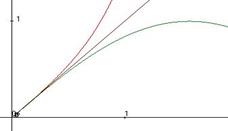
Неравенства 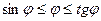перепишем в виде: .

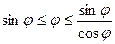Теперь разделим всё на синус. 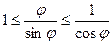. Рассмотрим обратные величины ко всем этим, пользуясь тем, что из 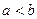следует 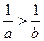. Получится .

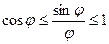Применим свойство, которое доказывали когда-то ранее: если 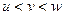и две крайние из 3 величин стремятся к А, то и средняя имеет предел и стремится к А.

Учитывая, что 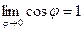, а константа справа и так равна 1, то .

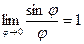Если обозначение угла сменить, обозначить x, то и получается .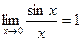

Следствия из 1-го замечательного предела:

, , , .

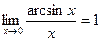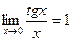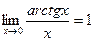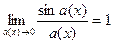Пример. .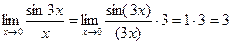

Более подробно: мы могли бы заменить 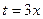, и учесть, что при 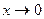будет и .

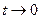Пример. Найти предел .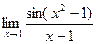

Решение. Надо получить в знаменателе такое же выражение, как под знаком sin.

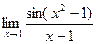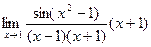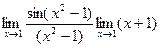= = = 2.

Здесь можно в процессе решения переобозначить 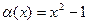, причём 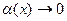при .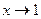

2-й замечательный предел.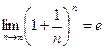

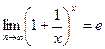
Обратите внимание, что этот предел вовсе не 1, как могло бы показаться. Ведь в степень всегда возводится не 1, а число, большее, чем 1. Оно уменьшается, но оно ни при каком n не равно 1. Здесь 2 процесса: одновременно уменьшается основание до единицы, и при этом увеличивается степень. Всё зависит от соотношения скоростей этих процессов.

Если, к примеру, есть 2 процесса: растворение краски и замораживание ёмкости с водой, то существенно отличается результат, если выполнить 1-й или 2-й процесс раньше. Если сначала заморозить воду, то уже ничего не растворится, а если сначала растворить, то будет равномерная смесь. Если замораживать одновременно с растворением, то будет другой результат, краска растворится не равномерно. Короче говоря, мы не имеем права считать, что сначала уменьшили основание в выражении 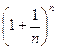и только потом стали увеличивать степень, здесь оба процесса идут одновременно, поэтому сказать, что такой предел всегда равен 1, будет ошибкой.

Число, даже очень близкое к 1, при возведении в выокую степень существенно возрастает. Так, при инфляции 10% в год, за 20 лет цена будет почти в 7 раз больше: 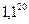= 6,7275. А если 15% в год, то за 20 лет в 16 раз больше: 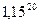= 16,36654.

Докажем, используя некоторые ранее полученные пределы, чтобы понять, каким образом в этом пределе появляется число e.

Возьмём выражение 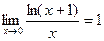, запишем как 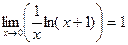.По свойству логарифма, 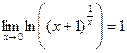. Возведём в степень e:

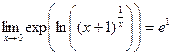, то есть .

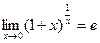Если ввести замену 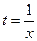, то получим 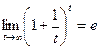. Если здесь выбрать значения только для целых абсцисс, то получится .

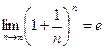Следствия из 2-го замечательного предела.

, , , .

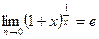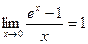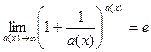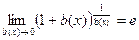Вообще, с помощью 2 замечательного предела можно раскрывать неопределённости вида .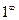

Пример. Вычислить предел .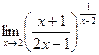

Решение. Заметим, что если отдельно рассмотреть основание, видно, что оно стремится к 1 (там получается 3/3). Степень стремится к бесконечности. Таким образом, здесь есть неопределённость вида 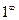, и можно применять 2-й замечательный предел.

Выделим целую часть этой неправильно дроби. Это можно сделать так: вписать перед дробью +1, а после неё (-1). Затем привести к общему знаменателю всё, что после первой единицы, то есть второй и третий элементы.

= =

= .

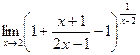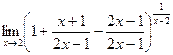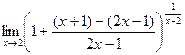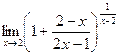Обратите внимание, что само собой автоматически получилось, что после 1 такая дробь, которая стремится к 0. Это и должно было получиться, ведь всё основание стремится к 1. Теперь нужно в степени искусственно домножить на дробь, обратную к той, что в основании следует после единицы. Но чтобы степень в примере не изменилась, надо компенсировать домножением и на саму эту дробь, а не только на обратную.

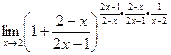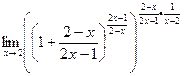= В больших скобках получилось выражение типа 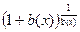, его предел равен e. Таким образом,

осталось найти = = = .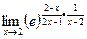

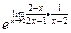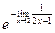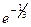Чтобы степени было видно крупнее, можно записать через exp(A) вместо e^A.

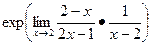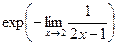= . Итак, .

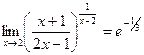* Замечание. Если основание стремится не к 1, а к другому числу, то второй замечательный предел можно и не использовать. Так, если 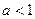то предел равен 0, если 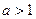то .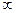

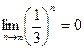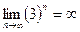, . Неопределённость возникает только в том случае, когда основание стремится к 1.