Главная часть бесконечно-малой.

Определение. Если 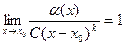то функция 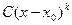называется ГЛАВНОЙ ЧАСТЬЮ бесконечно-малой .

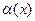Фактически, это степенная функция, эквивалентная данной 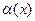. Если найти коэффициент 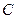и степень 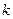, то мы найдём такую степенную функцию, график которой наилучшим образом (среди всех степенных) похож на график функции 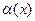в окрестности точки.

Пример. Найти главную часть бесконечно-малой 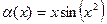в точке 0.

Решение. Так как точка 0, то 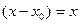, то есть главная часть имеет вид 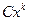. Запишем отношение данной бесконечно-малой и «эталонной» степенной. Нужно потребовать, чтобы этот предел был 1, ведь мы ищем именно эквивалентную бесконечно-малую.

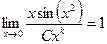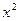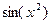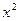. Преобразуем выражение с целью его упростить. Домножим и поделим на , этим мы фактически можем заменить на . Параметры C и k пока просто переписываем, не меняя их в процессе преобразований.

= .

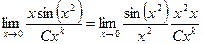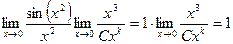Полное сокращение всех 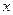будет лишь в случае k=3, а иначе предел 0 или 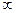, и не будет равен 1.

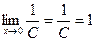, тогда С = 1. Итак, = .

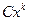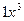Ответ. .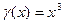

Ниже изображены графики бесконечно-малой и её главной части:

как видно, вблизи (0,0) они практически неотличимы.

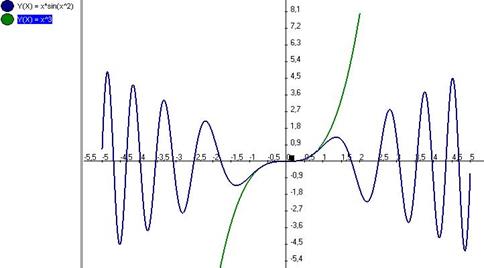
Задачи на поиск главной части по методам и сложности похожи на вычисление lim, но фактически это обратная задача: при вычислении предела внутри нет параметров, а предел неизвестен, здесь же наоборот, известно, что предел равен 1, но внутри выражения неизвестные параметры C, k, которые надо найти, так, чтобы предел был равен 1.

Если учесть не только одну степенную функцию, но добавить ещё и последующие степени, то можно построить ещё более точное приближение. Это будет изучено позже, тема «формула Тейлора».