ТЕПЛОПРОВОДНОСТЬ МНОГОСЛОЙНОЙ ПЛОСКОЙ

СТЕНКИ

В тепловых аппаратах часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов. Оценим темпе-ратурное поле и тепловой поток теплопроводностью через многослой-ную плоскую стенку, полагая, что все слои плотно прилегают друг к другу.

При стационарном тепловом режиме тепловые потоки через каждый из слоев будут одинаковыми, так как только при этом условии темпера-турное поле не изменяется с течением времени.

Для решения этой задачи рассмотрим трехслойную стенку, в которой толщина отдельных слоев равна δ₁, δ₂, δ₃, а их коэффициенты тепло-проводности соответственно λ₁, λ₂, λ₃ (рис. 2.5). На внешних поверх-ностях стенки поддерживаются постоянные температуры Т_с1 и Т_с2, причем Т_{с1 >} Т_с2; температуры на границах между слоями Т_сл1 и Т_сл2.

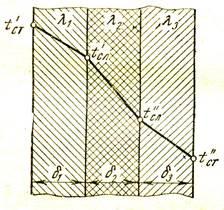
Рис. 2.5. Изменение температуры по толщине

многослойной плоской стенки

Выразим плотности тепловых потоков через отдельные слои с помощью формулы (2.23):

q = λ₁∙(Т_с1 – Т_сл1)/δ₁,

q = λ₂∙(Т_сл1 – Т_сл2)/δ₂, (2.25)

q = λ₃∙(Т_сл2 – Т_с2)/δ₃.

Перепишем эти уравнения в виде:

(Т_с1 – Т_сл1) = qδ₁/λ₁,

(Т_сл1 – Т_сл2) = qδ₂/λ₂, (2.26)

(Т_сл2 – Т_с2) = qδ₃/λ₃.

Просуммировав правые и левые части этих равенств, получим:

Т_с1 – Т_с2 = q(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃).

Откуда q = (Т_с1 – Т_с2)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃). (2.27)

Или для любой плоской многослойной стенки, состоящей из n слоев

_{i =n}

q = (Т_с1 – Т_с2) / ∑ δ_i/λ_i, (2.28)

^{i =1}

Здесь i – номер слоя.

_{i = n}

Величина ∑ δ_i/λ_i называется полным термическим сопротивлением

^{i = 1}

многослойной плоской стенки.

Зная плотность теплового потока через многослойную плоскую стенку, можно вычислить общее количество теплоты, которое переда-ется через наружную поверхность стенки F:

_{i =n}

Q = F∙(Т_с1 – Т_с2) / ∑ δ_i/λ_i, (2.29)

^{i =1}

Для построения температурного поля многослойной стенки необходимо оценить температуру на поверхности каждого слоя в отдельности. Система уравнений (2.26) позволяет получить расчетные формулы для определения температуры на поверхности любого слоя:

Т_сл1 = Т_с1 - qδ₁/λ₁,

Т_сл2 = Т_сл1 - qδ₂/λ₂, (2.30)

Т_с2 = Т_сл2 - qδ₃/λ₃.

Температура в каждом слое стенки при постоянном для слоя коэффициенте теплопроводности изменяется по линейному закону, а для многослойной плоской стенки в целом она представляет собой ломаную линию. Температурное поле многослойной стенки изображено на рис. 2.5. Наклон температурной линии в отдельных слоях различен. Это объясняется тем, что плотность теплового потока через каждый из слоев будет одинаковой:

q = - λ∙_·∂Т/∂x = const.

Поэтому слои с меньшим коэффициентом теплопроводности имеют больший температурный градиент ∂Т/∂x и, следовательно, больший наклон температурной линии.

При выводе формул для температурного поля и теплового потока теплопроводностью через многослойную плоскую стенку мы предполагали, что все слои плотно прилегают один к другому и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. В действительности на границе раздела двух слоев зачастую имеет место неплотное соприкосновение поверхностей. Это приводит к возникновению контактного термичес-кого сопротивления. В результате уменьшается тепловой поток тепло-проводностью через многослойную стенку.

Повышение сопротивления тепловому потоку в месте контакта двух поверхностей обусловлено меньшим коэффициентом теплопроводности газовой прослойки по сравнению с твердым телом, отклонением направления теплового потока от нормали к поверхности контакта, повышенным термическим сопротивлением поверхностного слоя из-за окисной пленки и загрязения. Надежные сведения о величинах контактного термического сопротивления получаются опытным путем.

Контактное термическое сопротивление существенно уменьшается при покрытии соприкасающихся поверхностей мягкими металлами (медь, олово и др.) или при прокладках из мягких материалов.