Аналитический способ определения равнодействующей плоской системы сходящихся сил

Пусть дана плоская система п сходящихся сил

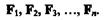
Равнодействующая этой системы

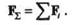
В плоскости действия данной системы выберем ось координат и спроеци­руем данные силы и их равнодействующую на эту ось.

Из математики известно свойство проекции векторной суммы, на ос­новании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е.

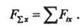
Правую часть этого равенства записываем упрощенно, а именно:

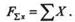
Для того чтобы определить равнодействующую любой плоской сис­темы сходящихся сил, спроецируем их на оси координат х и у, алгебраи­чески сложим проекции всех сил и найдем, таким образом, проекции рав­нодействующей:

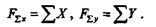
Зная проекции, на основании формул, полученных в § 2.3, определим модуль и направление равнодействующей: модуль равнодействующей

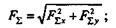
направляющий тангенс угла между вектором F 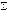и осью х

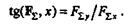
Линия действия равнодействующей проходит через точку пересече­ния линий действия составляющих сил.

Аналитические условия равновесия