ЦИЛИНДРИЧЕСКОЙ СТЕНКИ

Рассмотрим теплопроводность однородной цилиндрической стенки большой длины так, чтобы передачей теплоты с торцов трубы можно было пренебречь (рис. 2.6). Если внутренняя и внешняя поверхности поддерживаются при постоянных температурах Т_с1 и Т_с2, то тепловой поток имеет радиальное направление, а изотермические поверхности имеют форму цилиндров, у которых общая ось с трубой. В этих услови-ях температурное поле будет одномерным:

Т = f (r),

гдеr – текущая цилиндрическая координата.

На рис. 2.6 изображена цилиндрическая стенка длиной l, у которой внутренний радиус равен r₁, а наружный - r₂. Коэффициент теплопро-водности λ будем считать одинаковым для всей стенки.

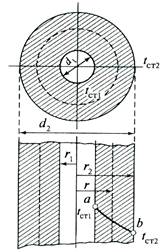
Рис. 2.6. Изменение температуры по толщине однослойной

цилиндрической стенки

Для стационарной одномерной задачи о теплопроводности цилиндрической стенки без внутренних источников теплоты дифферен-циальное уравнение теплопроводности (2.15) приводится к виду:

d²Т/dr² + 1/r ∙_·dТ/dr = 0. (2.31)

Введение новой переменной u = _·∂Т/∂ r позволяет привести уравнение (2.31) к виду:

du/d r + u/r = 0. (2.32)

Разделим переменные

du/u + d r/r = 0 (2.33)

и проинтегрируем

ln u + ln r = ln С₁. (2.34)

Потенцирование этого выражения ur = С₁, переход к первоначальным

координатам

dТ/d r ∙ r = С₁ или dТ = С₁ ∙ d r/r

и интегрирование дает

Т = С₁ ln r + С₂, (2.35)

где С₁ и С₂ – постоянные интегрирования.

Следовательно, распределение температур в стенке цилиндрической трубы представляет собой логарифмическую кривую.

Искривление линии температурного поля в цилиндрической стенке обусловлено изменением плотности теплового потока при изменении радиуса цилиндра: при уменьшении радиуса площадь поверхности, через которую проходит тепло, также уменьшается. Поэтому на малых радиусах температурная линия проходит более круто. Это правило остается в силе и при обратном направлении теплового потока (пунктир на рис. 2.6).

Для определения постоянных интегрирования С₁ и С₂ воспользуемся граничными условиями первого рода, т.е. зададимся законом распределения температур на наружной и внутренней поверх-ности цилиндрической стенки для любого момента времени:

при r = r₁ Т = Т_с1;

при r = r₂ Т = Т_с2.

Подставив эти эти выражения в уравнение (2.35), получим:

С₁ = (Т_с1–Т_с2)/ln (r₁/r₂); С₂ = Т_{с1 –} (Т_с1–Т_с2)∙ln r₁/ln (r₁/r₂). (2.36)

Заменив в (2.35) постоянные интегрирования найденными выражениями (2.36), получим уравнение стационарного температурного поля однородной цилиндрической стенки :

Т = Т₁ - (Т_{с1 –} Т_с2)∙ln (r/r₁) / ln (r₂/r₁), (2.37)

где r – переменный радиус.

Определим тепловой поток через изотермическую поверхность с радиусом r. В соответствии с законом Фурье:

Q = - λF_·dТ/dr = - λ2πrl∙_·dТ/dr. (2.38)

Из формулы (2.37) в результате вычисления производной от Т по переменному радиусу r получается следующее выражение для температурного градиента:

dТ/dr = - (Т_{с1 –} Т_с2)∙(1/r) / ln (r₂/r₁). (2.39)

После подстановки выражения (3.39) в (3.38) получим формулу для теплового потока:

Q = πl(Т_с1 – Т_с2) / (1/2λ) ln (r₂/r₁) =πl(Т_с1 – Т_с2) / (1/2λ) ln (d₂/d₁) . (2.40)

Если отнести тепловой поток к единице длины цилиндрической стенки, то формула (2.40) перепишется в виде:

q_l = π(Т_с1–Т_с2)/(1/2λ)ln (r₂/r₁) = π(Т_с1 – Т_с2)/(1/2λ) ln (d₂/d₁). (2.41)

Величину (1/2λ) ln (d₂/d₁) называют термическим сопротивлением цилиндрической стенки.

Обозначим плотности теплового потока на внутренней и внешней поверхностях через q₁ и q₂. Так как

Q = q_l l = q₁ 2πr₁ l = q₂ 2πr₂ l,

то

q_l = q₁ 2πr₁ = q₂ 2πr₂ . (2.42)

Отсюда плотность теплового потока:

на внутренней поверхности цилиндрической стенки

q₁ = q_l / 2πr₁ = (Т_с1 – Т_с2) / (r₁/λ)ln (r₂/r₁), (2.43)

на внешней поверхности цилиндрической стенки

q₂ = q_l / 2πr₂ = (Т_с1 – Т_с2) / (r₂/λ)ln (r₂/r₁). (2.44)

Если r₂/r₁ < 2, т.е. труба тонкостенная, то кривизна стенки слабо влияет на величину теплового потока. В этом случае (с точностью до 4%) для определения теплового потока , отнесенного к единице длины цилиндрической стенки, вместо выражения (2.41) можно использовать формулу плоской стенки:

q_l = 2 λ π r_cр(Т_с1 – Т_с2) / (r₂ - r₁), (2.45)

где r_cр – средний радиус цилиндрической стенки.