КОНВЕКТИВНЫЙ ТЕПЛООБМЕН ПРИ ВЫНУЖДЕННОМ ПРОДОЛЬНОМ ОБТЕКАНИИ ПЛОСКОЙ ПОВЕРХНОСТИ

2.3.1. Структура пограничного слоя

При течении среды у поверхности стенки образуется пограничный слой вязкой жидкости (рис.2.1). Движение жидкости в пограничном слое может иметь ламинарный и турбулентный характер, а толщина слоя постепенно возрастает по направлению движения жидкости.

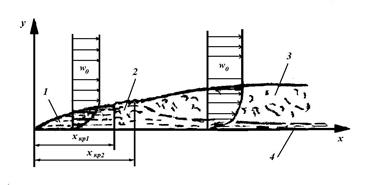
Рис. 2.1. Схема пограничного слоя:

1 – ламинарный пограничный слой; 2 – переходная область;

3 – турбулентный пограничный слой; 4 – вязкий (ламинарный) подслой

Переход ламинарного течения в турбулентное происходит на некотором участке Dх = х_кр1 - х_кр2. Эта область переходного течения не всегда может быть точно определена. Поэтому в расчетах часто полагают, что переход ламинарного течения в турбулентное происходит при определенном х_кр, т.е. заменяют отрезок Dх точкой, а критическое значение Re приближенно принимают равным 10⁵.

Тогда координата точки перехода ламинарного течения в турбулентное в пограничном слое может быть найдена следующим образом:

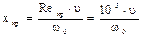(2.11)

2.3.2. Теплоотдача при ламинарном режиме движения в пограничном слое

В случае Re_ж ≤ 10⁵ режим движения жидкости ламинарный. Толщину гидродинамического δ_л и теплового К пограничных слоев на расстоянии Х от передней кромки пластины можно рассчитать по формулам:

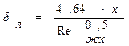(2.12)

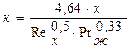(2.13)

Местный (локальный) коэффициент теплоотдачи определяется из следующих выражений:

при t_c=const

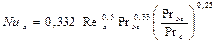(2.14)

при q_c=const

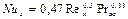(2.15)

где 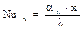; 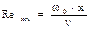- местные (локальные) значения чисел Нуссельта и Рейнольдса.

В этих уравнениях в качестве определяющего размера принимается координата точки х.

Средний коэффициент теплоотдачи при ламинарном режиме течения в пограничном слое:

при t_c=const

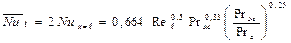(2.16)

при q_c=const

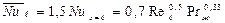(2.17)

В уравнениях (2.16) - (2.17) в качестве определяющего размера принимается длина пластины l, если вдоль всей поверхности течение ламинарное, или длина участка с ламинарным характером течения х_кр, если в пределах пластины происходит переход от ламинарного движения к турбулентному.

2.3.3. Теплоотдача при турбулентном режиме движения в пограничном слое

Если Re_ж > 10⁵, режим движения жидкости турбулентный. В этом случае толщина динамического и теплового пограничных слоев совпадает и определяется по формуле

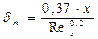(2.18)

Для вычисления местного коэффициента теплоотдачи справедливы следующие расчетные соотношения:

при t_c=const

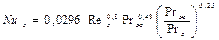; (2.19)

при q_c=const

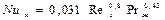. (2.20)

Средняя теплоотдача в обоих случаях рассчитывается по формуле

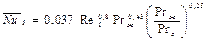. (2.21)

Физические параметры, входящие в числа подобия, выбираются по температуре набегающего потока t_ж, число Прандтля Pr_с – по температуре t_c.

2.4. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ЖИДКОСТИ В ТРУБАХ

При движении теплоносителей в трубах принято два критических значения числа Рейнольдса: Re_кр1=2300 и Re_кр2=10000.

Если Rе < 2300 - режим движения ламинарный,

Rе > 10000 - режим движения турбулентный,

2300 < Re < 10000 - переходный режим движения.

2.4.1. Теплоотдача при ламинарном режиме движения

При значениях Rе < 2300 (ламинарный режим движения) может возникать свободная конвекция. При этом течение может быть вязкостное (только вынужденная конвекция) или вязкостно-гравитационное (одновременно вынужденная и свободная конвекция).

При ламинарном вязкостном движении жидкости в трубах рекомендуется уравнение (Gr Pr < 8 10⁵)

Nu_d = 1,55(Re_d Pr_ж d/ 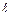)^0,33(m_ж/m_с)^0,14_, (2.22)

Значения физических свойств выбираются по средней температуре пограничного слоя жидкости.

При ламинарном вязкостно-гравитационном движении число Нуссельта можно рассчитать по уравнению

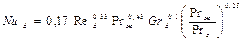(2.23)

Значения физических свойств выбираются по средней температуре жидкости.

2.4.2. Теплоотдача при турбулентном режиме движения

При турбулентном режиме течения теплоносителя внутри трубы (Re >10000) расчет числа Нуссельта и соответственно коэффициента теплоотдачи ведется по уравнению

Nu_d = 0,021Re_d^0,8 Pr_ж^0,43(Pr_ж/Pr_с)^0,25 e 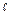, (2.24)

где e 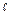- поправка на начальный участок_, учитывает изменение a

по длине канала.

2.4.3. Теплоотдача при переходном режиме движения

Если режим течения переходный (2300<Re<10000), рекомендуется уравнение

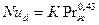(2.25)

где "К" определяется как функция числа Рейнольдса из данных табл.

Таблица 2.1.

2.4.4. Теплоотдача при течении в каналах некруглого поперечного сечения

При течении потока в трубах и каналах в качестве определяющего размера принимают

- для трубы круглого сечения внутренний диаметр d₁;

- для каналов некруглого сечения эквивалентный диаметр

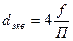, (2.26)

где ƒ- площадь поперечного сечения канала, м²;

П. - периметр этого сечения, м.

Например:

- для канала квадратного сечения

d_экв = α (α - сторона квадрата);

- для канала прямоугольного сечения

(α и в - стороны прямоугольника);

- при внешнем продольном обтекании трубных пучков

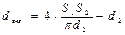
(S₁ и S₂ – шаги труб).

- для кольцевого канала

d_экв = Д - d₂ ( Д - внутренний диаметр наружной трубы,

d₂ - наружный диаметр внутренней трубы).

Аналогичные зависимости для определения коэффициента теплоотдачи имеются для других условий теплообмена (конденсации, кипения, внешнего обтекания пучков труб и др.)

2.5. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН ПРИ СВОБОДНОМ ДВИЖЕНИИ ЖИДКОСТИ

Свободная конвекция возникает за счет неоднородного распределения в среде массовых (объемных) сил. Такими силами являются сила тяжести, центробежная сила и силы за счет наведения в жидкости электромагнитного поля высокой напряженности. В дальнейшем будет рассмотрена теплоотдача только при свободном гравитационном движении.

В уравнении движения гравитационные силы (силы тяжести). учитываются членом 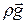. При теплообмене причиной, вызывающей движение, является разность температур между поверхностью теплообмена и окружающей средой Т.к. температура жидкости переменна, возникает разность плотностей в различных точках объема и, как следствие, разность гравитационных сил, представляющих собой архимедову или подъемную (опускную) силу.

Около горячей поверхности ( 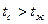) жидкость становится легче и поднимается вверх, на ее место поступает более холодная (с большей плотностью). При этом теплота, воспринимаемая жидкостью от поверхности, переносится в окружающее пространство.

Интенсивность теплоотдачи при свободной конвекции зависит от следующих факторов:

1) разности температур тела и среды,

2) протяженности поверхности в направлении вертикальной оси,

3) физических свойств и природы среды,

4) положения нагретой поверхности в пространстве (форма несущественна);

5) величины пространства, в котором развивается свободная конвекция.

Свободное движение может быть ламинарным и турбулентным. Режим движения определяют по числу подобия Рэлея, представляющему собой произведение чисел Грасгофа и Прандтля

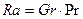. (2.27)

При малых размерах поверхности и температурных напорах ( 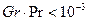) около поверхности образуется неподвижная пленка нагретой среды – такой режим называется пленочным, при этом свободная конвекция отсутствует, а перенос теплоты через пристенный пограничный слой происходит теплопроводностью.

При 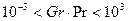появляются конвективные токи – этот режим является переходным от пленочного к ламинарному.

Если 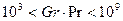- то возникает ламинарный режим свободного движения.

Переходный режим от ламинарного к турбулентному имеет место при 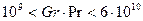, он характеризуется неустойчивостью процесса течения и теплоотдачи.

Развитое турбулентное течение наступает при значениях .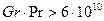

В общем случае при 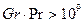расчет ведётся по уравнениям для турбулентного режима течения.

Теплоотдача при свободной конвекции зависит от того, как поверхность ориентирована в пространстве.

2.5.1. Конвективный теплообмен при свободном движении жидкости около вертикальной поверхности

Значение коэффициента теплоотдачи при свободном движении около вертикальных поверхностей в условиях, когда 10³ < Gr_ж Pr_ж < 10⁹ (ламинарный режим), определяется из выражения

Nu_h = 0,75 (Gr_h Pr_ж)^0.25 (Pr_ж / Pr_с)^0,25, (2.28)

Если Gr_жPr_ж > 10⁹ (турбулентный режим), то

Nu_h=0,15 (Gr_h Pr_ж)^0.33 (Pr_ж / Pr_ж)^0.25. (2.29)

Определяющей температурой, по которой выбираются значения физических параметров, является температура среды вдали от стенки. В качестве определяющего размера принимается высота h.

2.5.2. Конвективный теплообмен при свободном движении жидкости около горизонтальных труб

Характер свободного движения около горячих горизонтальных труб представлен на рисунке 1.

Рис. 1. Свободное движение около горизонтальных труб

Около горизонтальных труб небольшого диаметра в широком интервале изменения температурного напора 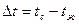сохраняется ламинарное движение жидкости, так как поверхность имеет небольшую протяженность по высоте. При прочих равных условиях чем больше диаметр труб, тем вероятнее разрушение ламинарного течения.

Для расчета среднего коэффициента теплоотдачи при свободном движении жидкости около нагретых горизонтальных труб в условиях, когда 10³ < Gr_ж Pr_ж < 10⁹, рекомендуется следующее уравнение подобия

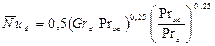, (2.30)

Определяющей температурой, по которой выбираются значения физических параметров, является температура среды вдали от поверхности трубы. В качестве определяющего размера принимается наружный диаметр трубы.

2.5.3. Конвективный теплообмен при свободном движении жидкости около горизонтальной плоской поверхности

Для расчета средних коэффициентов теплоотдачи при свободном ламинарном движении около горизонтальной плоской поверхности может быть использована формула ():

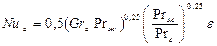, (2.31)

В качестве определяющего размера берется меньшая сторона поверхности – .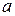

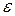- поправка, учитывающая положение плоской поверхности.

При обращении горячей поверхности вниз .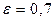

При обращении горячей поверхности вверх .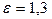

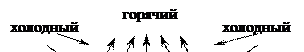
Рис. 2. Свободное движение около горизонтальной поверхности