СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

В стационарных процессах теплопроводности температура в любой точке твердого тела не зависит от времени, т.е. ∂Т/∂t =0.

В настоящей главе рассматриваются наиболее распространенные простейшие стационарные задачи теплопроводности при условии, что тепловыделение (теплопоглощение) в объеме стенок отсутствует, т.е. q_v=0. В этом случае дифференциальное уравнение теплопроводности после сокращения коэффициента температуропроводности принимает вид:

в прямоугольных координатах x, y, z

Ѳ Т = ∂²Т/∂x² + ∂²Т/∂y² + ∂²Т/∂z² = 0; (2.14)

в цилиндрических координатах r, j, z

Ѳ Т= ∂²Т/∂r² + 1/r ∙_·∂Т/∂ r + 1/r² ∙ ∂²Т/∂j² + ∂²Т/∂z² = 0. (2.15)

ТЕПЛОПРОВОДНОСТЬ ОДНОСЛОЙНОЙ ПЛОСКОЙ

СТЕНКИ

Рассмотрим температурное поле и тепловой поток при стационарной теплопроводности через однослойную плоскую стенку, площадь боковой поверхности которой настолько велика, что теплообменом через ее торцы можно пренебречь. Участок такой стенки изображен на рис. 2.4. Стенка имеет толщину δ и одинаковый для всей стенки коэффициент теплопроводности λ. Температуры на границах стенки Т_с1 и Т_с2 поддерживаются постоянными, а изотермические поверхности имеют форму плоскостей, параллельных поверхностям стенки. Температура меняется только в направлении, перпендикулярном к плоскости стенки, которое принимаем за ось x. При рассматриваемых условиях теплота может распространяться только вдоль оси x, и температурное поле будет одномерным. Температурные градиенты вдоль остальных осей координат равны нулю:

∂Т/∂y = ∂Т/∂z = 0 и ∂²Т/∂y² = ∂²Т/∂z² = 0. (2.16)

Поэтому дифференциальное уравнение теплопроводности (2.14) приводится к виду:

d²Т/dx² = 0 . (2.17)

Проинтегрировав это уравнение дважды, найдем:

dТ/dx = С₁, (2.18)

Т = С₁x + С₂, (2.19)

где С₁ и С₂ – постоянные интегрирования.

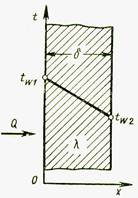
Рис.2.4. Изменение температуры по толщине

однослойной плоской стенки

Следовательно, температурное поле однослойной плоской стенки при постоянном коэффициенте теплопроводности выражается линейной зависимостью температуры от координаты (рис. 2.4).

Для определения постоянных интегрирования С₁ и С₂ воспользуемся граничными условиями первого рода, т.е. зададимся законом распределения температур на поверхности тела для любого момента времени:

при x = 0 Т = Т_с1;

при x = δ Т = Т_с2.

Подстановка этих условий в уравнение (2.19), дает:

С₂ = Т_с1; С₁ = (Т_с2 – Т_с1)/δ. (2.20)

Заменив в (2.19) постоянные интегрирования найденными выражениями (2.20), получим уравнение стационарного температурного поля однослойной плоской стенки:

Т = (Т_{с2 –} Т_с1)∙_·x/δ + Т₁. (2.21)

Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства (2.18) можно записать:

q = - λ∙_·∂Т/∂x = - λС₁ = - λ∙(Т_с2 – Т_с1)/δ. (2.22)

Или

q = λ∙(Т_с1 – Т_с2)/δ. (2.23)

Зная плотность теплового потока через плоскую стенку, можно вычислить общее количество теплоты, которое передается через поверхность стенки F:

Q = λF∙(Т_с1 – Т_с2)/δ. (2.24)

Следовательно, количество теплоты, передаваемое теплопроводностью через однослойную плоскую стенку, прямо пропорционально коэффи-циенту теплопроводности стенки, её площади, разности температур на-ружных поверхностей стенки и обратно пропорционально толщине стенки.

Соотношение λ/δ называется тепловой проводимостью плоской стенки, а обратная величина δ/λ – термическим сопротивлением плоской стенки.