Вычисление площади плоской фигуры
Площадь криволинейной трапеции, ограниченной кривой 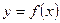
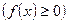 , прямыми
, прямыми 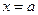 и
и 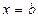 , и отрезком
, и отрезком 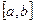 оси Ох, вычисляется по формуле:
оси Ох, вычисляется по формуле:
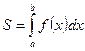 .
.
Площадь фигуры, ограниченной кривыми 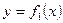 ,
, 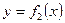
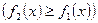 и прямыми
и прямыми 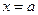 ,
, 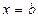 , вычисляется по формуле:
, вычисляется по формуле:
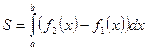 .
.
Пример 9.Найти площадь плоской фигуры, ограниченной параболой 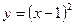 и гиперболой
и гиперболой 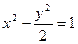 .
.
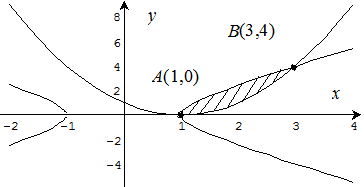
Рис. 3
Найдем точки пересечения параболы и гиперболы, для чего решим совместно уравнения этих кривых:
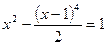
или
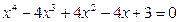 .
.
Левую часть последнего уравнения можно разложить на множители
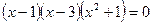 ,
,
откуда 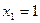 ,
, 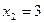 и
и 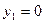 ,
, 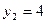 . Таким образом, заданные кривые пересекаются в точках
. Таким образом, заданные кривые пересекаются в точках 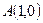 и
и 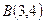 (см. рис. 3). Следовательно,
(см. рис. 3). Следовательно,
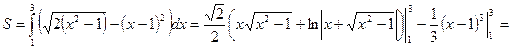
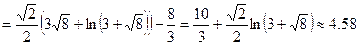 .
.
Вычисление объема тела вращения
Если криволинейная трапеция, ограниченная кривой 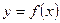 и прямыми
и прямыми 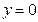 ,
, 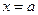 ,
, 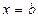 , вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле
, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле
 .
.
Если фигура, ограниченная кривыми 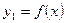 ,
, 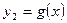
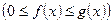 и прямыми
и прямыми 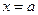 ,
, 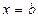 вращается вокруг оси Ох, то объем тела вращения
вращается вокруг оси Ох, то объем тела вращения
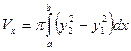 .
.
Пример 10.Вычислить объем тела, образованного вращением относительно оси Ох фигуры, ограниченной кривыми 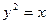 и
и 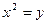 (рис. 5).
(рис. 5).
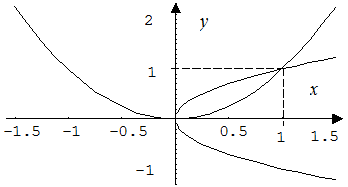
Рис. 5
Определяем точки пересечения данных кривых. Для этого решаем уравнение 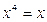 , откуда
, откуда 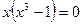 , т.е.
, т.е. 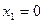 ,
, 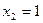 . Следовательно,
. Следовательно,
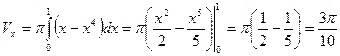 .
.
Дата добавления: 2021-01-26; просмотров: 598;











