Длина дуги плоской кривой
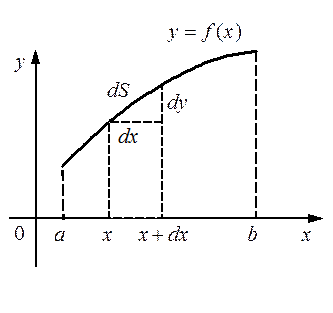 Пусть кривая описывается уравнением
Пусть кривая описывается уравнением 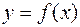 . Рассмотрим дугу этой кривой при
. Рассмотрим дугу этой кривой при  . Обозначим длину этой дуги через
. Обозначим длину этой дуги через  . Предположим, что на промежутке
. Предположим, что на промежутке 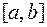 существует непрерывная производная
существует непрерывная производная 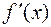 .
.
Чтобы вычислить длину дуги, выделим на дуге элементарный участок, соответствующий изменению аргумента 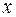 на промежутке
на промежутке 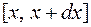 . Обозначим бесконечно малый элемент длины дуги
. Обозначим бесконечно малый элемент длины дуги 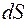 . Вычислим
. Вычислим 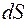 , заменив бесконечно малую дугу её хордой, величину
, заменив бесконечно малую дугу её хордой, величину  величиной
величиной 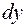 и применив теорему Пифагора.
и применив теорему Пифагора.
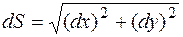
или
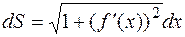 .
.
Тогда
 .
.
Замечание. Если дуга кривой описана уравнением 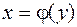 ,
, 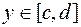 , то получим
, то получим
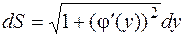
и
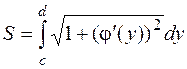 .
.
Если же дуга описывается параметрически
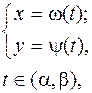
то

и
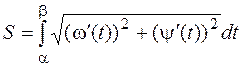 .
.
.
Вычисление площади поверхности тела вращения
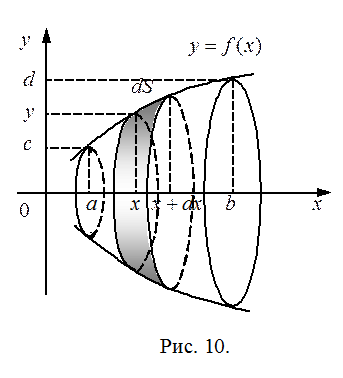 Рассмотрим поверхность, образованную вращением вокруг оси
Рассмотрим поверхность, образованную вращением вокруг оси 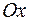 дуги кривой
дуги кривой 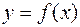 (рис. 10). Предположим, что функция
(рис. 10). Предположим, что функция 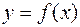 имеет непрерывную производную
имеет непрерывную производную 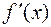 при всех
при всех  . Будем искать площадь поверхности
. Будем искать площадь поверхности 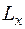 , отсеченной плоскостями
, отсеченной плоскостями 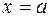 ,
, 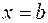 . Для этого выделим на дуге
. Для этого выделим на дуге 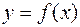 элемент, соответствующий изменению абсциссы от
элемент, соответствующий изменению абсциссы от 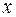 до
до 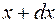 , и будем его вращать.
, и будем его вращать.
В качестве бесконечно малого элемента 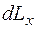 примем площадь боковой поверхности усеченного конуса с образующей
примем площадь боковой поверхности усеченного конуса с образующей 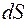 и радиусом среднего сечения
и радиусом среднего сечения  , где
, где  – ордината, соответствующая абсциссе
– ордината, соответствующая абсциссе 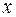 .
.
Действительно,
 .
.
Однако вторым слагаемым в последней части равенств можно пренебречь как бесконечно малой величиной более высокого порядка малости, чем 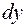 . Тогда
. Тогда
 .
.
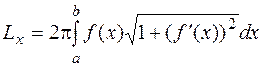 .
.
Замечание 1. Если дуга кривой описана уравнением 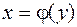 ,
, 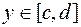 , то получим
, то получим
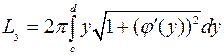 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Максимум и минимум функции | | | Системы защиты в торговых предприятиях |
Дата добавления: 2020-04-12; просмотров: 626;











