Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности)

Считаем, что течение происходит по закону Дарси, и уравнение состояния упругой жидкости в линеаризированной постановке, которое получим из соотношения (2.27) 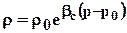разложением экспоненты в ряд Тейлора, имеет вид

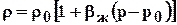, (5.8)

а также изменение пористости в зависимости от давления, полученное линеаризацией соотношения (2.34) 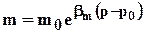, описывается зависимостью

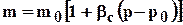. (5.9)

Из (5.9) и очевидного соотношения 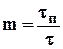имеем следующее дифференциальное уравнение для пористости, при пренебрежении членом, содержащим произведение b_жb_с

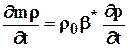. (5.10)

В тоже время из общего уравнения фильтрации (2.8) .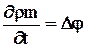

Приравнивая правые части, с учетом выражения для потенциала 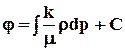, и пренебрегая членом, содержащим (р-р₀)², получим

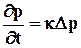. (5.11)

Уравнение типа (5.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент k характеризует быстроту распределения давления в пласте и носит название коэффициент пьезопроводности. Само уравнение (5.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.