Этап 2. Расчет напряжений в узлах сети

Исходными данными при этом служат заданное напряжение U_A источника питания и найденные на предыдущем этапе расчета мощности в начале каждого участка сети.

1. Определяем ток головного участка сети по данным начала звена

2. Вычисляемпадениенапряжения на головном участке

или эта же величина, определяемая через поток головного участка:

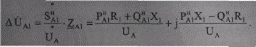
3. Находим в соответствии с указанным направлением тока I_а1 напряжение в узле 1:

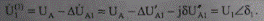(6.38)

На рис. 6.8 приведена векторная диаграмма напряжений, соответствующая выражению (6.38). Из диаграммы определяют величину (модуль) напряжения в узле 1:

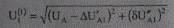
и фазу (аргумент) этого напряжения:

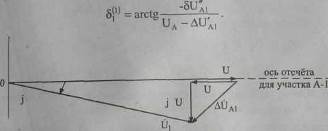
Рис. 6.8. Векторная диаграмма напряжений для головного участка сети

Расчет напряжений в других узловых точках сети выполняют аналогично. В частности,

для концевого участка сети напряжение НН, приведенное к ВН

вычисляют через значение модуля вектора напряжения U₂ получаемого в ре­зультате совмещения с осью отсчета аргументов (осью вещественных величин). Причем фазовый угол δ₃ равен сумме углов между векторами напряжений сосед­них узловых точек и определяется выражением вида (6.37). На рис. 6.9 приведена векторная диаграмма напряжений данной сети при заданном напряжении U_A в источнике питания.

Второй этап завершает расчет режима сети в первом приближении. Уточне­ние параметров электрического режима можно выполнить на второй итерации по рассмотренному алгоритму расчета, заменив начальное приближение напряжения U⁽⁰⁾_I на вычисленное U⁽¹⁾_I в первом приближении. Формально окончание расчета можно контролировать вычислением критерия вида (5.75) для наиболее удален­ной узловой точки 3:

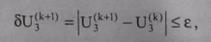
т. е. вычисления будут повторяться до тех пор, пока значение искомой перемен­ной U₃ на двух смежных итерациях не будет отличаться на сколь угодно малую, наперед заданную величину ε. Однако практически достаточно для неперегруженных разомкнутых сетей выполнить одно-два приближения (итерации) рас­смотренного расчета.

Зная напряжение U₃, определим фактическое напряжение на шинах НН подстанции, например, при номинальном коэффициенте трансформации k_т:

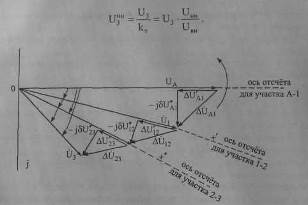
Рис. 6.9. Векторная диаграмма напряжений для сети из трех последовательных участков (расчет по данным в начале сети)

В итоге отметим, что при расчете режимов слабозагруженных сетей 110 кВ и сетей меньших номинальных напряжений общие расчетные формулы, приве­денные в данном параграфе для определения напряжений в узловых точках сети, можно упростить. Поперечная составляющая падения напряжения

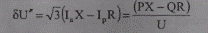
и соответственно фазовый сдвиг напряжений (6.39), например, при передаче по сети активно-индуктивной мощности, имеет незначительную величину (см. параграф 5.2). Поэтому ее влияниена модуль напряжения]

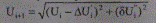
не учитывается, так как практически лежит в пределах точности расчета, а расчет напряженийведется по упрощенным формулам вида (5.38).

Вопросы для самопроверки

1. В чем состоит отличие расчетов электрического режима линии электро­передачи и продольного звена?

2. Каковы характерные случаи расчета электрического режима линии?

3. В каких случаях и почему расчет режима линии реализуется точной (пря­мой) и приближенной (итерационной) процедурой?

4. Когда расчет режима линии выполняют в два этапа? Что анализируют на каждом этапе?

5. Каковы расчетные выражения алгоритмов анализа режима линии точным и приближенным методами?

6. В чем заключается точный и приближенный алгоритмы расчета режима линии в токах?

7. В чем проявляется влияние активной и емкостной проводимостей ЛЭП на потери мощности и напряжение?

8. В каком случае для расчета режима линии достаточно 1—2 итераций? Что ухудшает сходимость расчета?

9. Когда возникает режим холостого хода? В чем состоит его особенность для протяженных линий?

10. Что определяет режим холостого хода ЛЭП? Почему напряжение в кон­це линии превышает напряжение в ее начале?

11. Как получить зависимость превышения напряжения в режиме холостого хода линии от ее протяженности?

12. Изобразите векторную диаграмму напряжений в режиме холостого хода ЛЭП. В чем причина отставания по фазе вектора напряжения в конце линии от вектора напряжения в ее начале?

13. Сформулируйте алгоритм анализа режима холостого хода протяженных ЛЭП.

14. Какие электрические сети называются разомкнутыми?

15. Чем определяется рабочий (установившийся) режим электрической сети?

16. Какие исходные данные необходимы для выполнения расчета устано­вившегося режима сети?

17. Какие методы чаще всего используют для расчета установившихся ре­жимов простейших сетей?

18. Как влияют данные о нагрузке и напряжениях в узлах на последователь­ность расчета режима разомкнутой сети?

19. Какова последовательность расчета режима разомкнутой сети при зада­нии напряжения в ее конечном узле?

20. В чем сущность метода расчета режима разомкнутой сети «в два этапа»?

21. Какое допущение принимается при расчете режима разомкнутой сети на первом этапе?

22. В каких случаях при расчете методом последовательных приближений можно ограничиться одной-двумя итерациями?

23. В каких случаях можно вести расчет напряжений в узлах разомкнутой сети без учета поперечной составляющей вектора падения напряжения?

24. Каким образом учитываются поперечные ветви (шунты) при расчете ре­жима разомкнутой сети?

25. Как найти фазовый угол напряжения узла, наиболее удаленного от ба­лансирующего?

26. Как определить КПД линии электропередач при задании нагрузки в ее начале и конце?