ГЛАВА 8. ОСНОВЫ РАСЧЕТА УСТАНОВИВШИХСЯ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ НА ЭВМ
Выше рассмотрены традиционные (ручные) инженерные методы расчета параметров установившихся (стационарных) режимов простейших электрических сетей (ЭС)
Расчет и анализ электрических режимов реальных ЭС и систем передачи и распределения электроэнергии, содержащих десятки, сотни линий электропередачи и узлов нагрузки, необходимо выполнять посредством программно-вычислительных комплексов на ЭВМ.
Большая размерность и сложность исследуемой задачи, необходимость ее многократного решения, зачастую с требованием высокой скорости и надежности получения решения, обуславливают использование программно-вычислительного аппарата как эффективное (в ряде случаев единственное) средство решения широкого множества задач эксплуатации, проектирования и исследования электроэнергетических систем (ЭЭС), сетей и систем передачи и распределения электрической энергии.
Ниже рассматриваются теоретические основы и примеры практической постановки и решения задачи расчета установившихся режимов ЭС (и, в более общем случае, ЭЭС) с применением математических моделей и численных методов, реализуемых на ЭВМ.
Расчет установившихся режимов ЭС содержит два этапа: формирование уравнений и их решение. Математическое описание (математические модели) в виде уравнений установившихся режимов, методы их решения и особенности их реализации в практических алгоритмах описаны в многочисленной литературе, в частности [44—48, 53, 55—59].
8.1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ И ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДОВ РЕШЕНИЯ
Расчет установившихся режимов (состояний) ЭС в классическом виде заключается в определении напряжений в узлах сети, используя которые, находят потокораспределение и потери мощности. Математически эта задача формулируется как решение системы нелинейных алгебраических или тригонометрических уравнений, описывающих режим. В основе такого описания состояния ЭС лежат законы Кирхгофа и Ома, устанавливающие связи между токами, напряжениями и параметрами сети. Непосредственно применение уравнений Кирхгофа неэффективно и в алгоритмах для ЭВМ не используется. Для построения соответствующих алгоритмов электрического расчета наиболее эффективными и удобными для реализации на ЭВМ являются уравнения узловых напряжений (потенциалов), связывающие напряжения в узлах ЭС и мощности (токи), подводимые к этим узлам, через параметры схемы [8, 50].
Уравнения узловых напряжений (УУН) следуют из первого закона Кирхгофа в результате представления по закону Ома токов во всех ветвях через узловые напряжения и проводимости ветвей. Вывод и свойства этих уравнений даны, например, в [46, 47]. Дадим краткую характеристику формам и способам записи УУН.
8.1.1. Математическая постановка задачи
Нелинейные уравнения узловых напряжений.При расчетах электрических режимов ЭЭС на ЭВМ целесообразно использовать наиболее точные модели электрических нагрузок. Узловые нагрузки генераторов и потребителей задаются их нелинейной зависимостью от узловых напряжений (5.2) в виде узлового тока (нелинейного источника тока), т. е.
|
Отмеченная нелинейность проявляется при представлении в узлах нагрузки потребителей или генераторов неизменной мощностью (4.35)
|
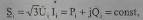
либо при задании нагрузок потребителей их статическими характеристиками (4.24)
|
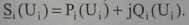
Если во всех n узлах (кроме балансирующего, имеющего номер n+1) заданы нагрузки указанными моделями, то для ЭС трехфазного переменного тока имеем систему n нелинейных УУН с комплексными коэффициентами. Различают две формы таких уравнений: уравнения баланса токов (5.3)
|
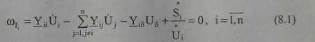
и баланса мощностей (5.4)
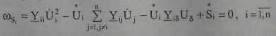(8.2)
Эти же уравнения в матричной записи имеют вид:
Уравнения баланса токов
(8.3)
Уравнение баланса мощностей
(8.4)
Заметим, что в выражениях (8.1) — (8.4) значения токов в √З раз превышают реальные фазные токи. Такая запись несколько упрощает систему УУН и поэтому является общепринятой [8, 46].
В данных уравнениях функции ωIi,. ωSi, комплексных переменных напряжений узлов соответствуют небалансу полного тока или полной мощности в i-м узле; n+1 — число узлов ЭС, включая балансирующий с заданным напряжением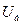 
неизменной фазой δ, равной нулю; U,S—n-мерные вектор-столбцы узловых междуфазных напряжений 
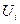и комплексно-сопряженных нагрузок Si в узлах; diag 
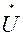— диагональная матрица сопряженных комплексов напряжений Ui; Y - матрица собственных и взаимных проводимостей с комплексными элементами Yij; Y6 — вектор-столбец, i-й элемент которого равен Yi6.
Матрица собственных и взаимных проводимостей узловY, играющая важную роль при формировании уравнений установившихся режимов, обладает следующими свойствами:
(8.4 а)
где Xij — собственная проводимость узла i, Yij — взаимная проводимость узлов i и j, определяемая продольным сопротивлением ветви Zij; Yi0 — результирующая проводимость узла i на землю. В общем случае принято, что
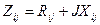
активно-индуктивный элемент. Тогда полагаем для собственных проводимостей узлов
для взаимных проводимостей
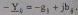
С учетом комплексных коэффициентов трансформации kij
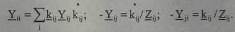
матрица Y теряет свойства симметричности.
Матрица Y для реальных ЭС, содержащих десятки и сотни узлов, является сильно разреженной (слабо заполненной); заполненность матрицы Y, как правило, не превышает 2—5 %.
Простота расчета элементов матрицы Y в соответствии с (8.4 а), учет свойств
симметричности и разреженности матрицы обуславливают алгоритмические удобства формирования УУН и эффективность процедуры их решения, что в итоге и определяет широкое применение УУН при расчетах установившихся режимов реальных ЭС на ЭВМ.
Для построения алгоритмов расчета параметров установившегося режима на ЭВМ необходимо оперировать УУН с вещественными величинами. Предварительное преобразование системы уравнений необходимо из-за отсутствия производной комплексно-сопряженной величины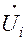 
, входящей в уравнения (8.1) по прямому Ui и сопряженному комплексу Ui (8.2) [8, 46]. Существуют два способа записи вещественных УУН: в прямоугольных и полярных координатах.
УУН в прямоугольной (декартовой) системе координат. Примем комплексные величины в виде
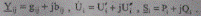(8.5)
В результате замены комплексов через их составляющие и выполнения несложных алгебраических преобразований в уравнениях (8.1) и (8.2), выделив в них отдельно действительные имнимые составляющие небалансов токов
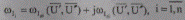
и небалансов мощностей
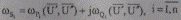
получим следующие системы нелинейных уравнений двойного порядка с вещественными коэффициентами:
в форме баланса активных и реактивных составляющих токов
(8.6а)
(8.6б)
и в форме баланса активных и реактивных мощностей:
(8.7а)
(8.7б)
Где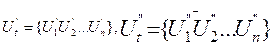 
— векторы действительных и мнимых составляющих напряжений, относительно которых решаются данные системы нелинейных уравнений.
УУН в полярной системе координат. Вданной системе координат формируются УУН, в которых напряжения узлов представляются своими модулями (значениями) U = {U, /i = 1, n) и фазами напряжений δ = δi /i = 1, n} по отношению к напряжению балансирующего узла. Связь между представлениями напряжений в полярной и прямоугольной системе координат определяется следующими формулами прямого и обратного преобразований [46]:
|
Выполним замену комплексных величин в уравнениях (8.1) и (8.2) их соответствующими значениями в полярной (экспоненциальной) форме
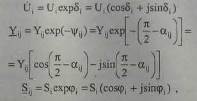
где Ui ,Yij,Si- модули соответствующих комплексных величин; ψij=arctgbij/gij; αij=arctg gij/bij.
В результате перехода к тригонометрической форме представления комплексных чисел, сгруппировав раздельно действительные и мнимые составляющие небалансов токов
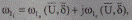
и небалансов мощностей
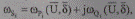
получим следующие системы вещественных уравнений двойного порядка в полярной системе координат:
в форме баланса активных ωia, и реактивных ωir, составляющих токов
(8.8a)
(8.8б)
и в форме баланса активных и реактивных мощностей
(8.9а)
(8.9б)
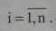
Полученные системы УУН (8.8) и (8.9) нелинейные относительно искомых модулей U и фаз δ напряжений.
Таким образом, имеем четыре формы записи УУН (8.6) — (8.9). Переход от комплексных УУН к действительным как в форме баланса токов, так и в форме баланса мощностей приводит в общем случае к увеличению в 2 раза размерности систем нелинейных уравнений установившегося режима.
В отдельных случаях, в частности, при анализе режимов распределительных ЭС, нагрузки в узлах могут быть заданы неизменными модулями тока Ii и коэффициентом мощности cosφi. Тогда нелинейные зависимости выражений для тока в УУН (8.6)
(8.10)
и в УУН (8.8)
(8.11)
заменяются неизменными значениями составляющих токов
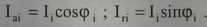
В результате такой замены нелинейные УУН (8.6) преобразуются в систему линейных алгебраических уравнений и в целом снижается трудоемкость решения УУН в форме баланса токов.
Функции ωia, ωir, ωP, ωQ описывающие небалансы (невязки) активных и реактивных составляющих токов или мощностей в узлах сети, определяются как результат подстановки очередного (k-гo) приближения искомых переменных
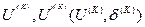в приведенные уравнения или, иначе, как разность между расчетными и узловыми (заданными) значениями токов
|
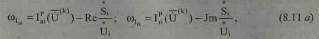
или мощностей
(8.11б)
Данные математические модели применимы для описания ЭС, не содержащих в своем составе генерирующих источников, кроме балансирующего по активной и реактивной мощности (станция, ведущая по частоте, узел типа U,δ). Во всех других п узлах нагрузки учтены, как правило, значениями требуемой активной и реактивной мощности, принимаемых либо постоянными, либо изменяющимися в соответствии со статическими характеристиками (узлы типа Р, Q). В последнем случае выполняется корректировка мощностей нагрузок в зависимости от изменения модуля напряжения в итерационном процессе решения УУН.
Учет опорных узлов типа Р, U — const.В части генераторных узлов ЭЭС необходимо учесть заданные активную мощность Р, и модуль напряжения, которые регулируются и могут быть фиксированными (опорные узлы типа Р, U). Такие узлы, представляющие большинство генераторов электростанций с первичным регулированием частоты, являются базисными по напряжению и балансирующими по реактивной мощности Qi пределы изменения которой (располагаемая реактивная мощность)
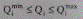(8.12)
задаются константами, определяемыми допустимой нагрузкой статорной и роторной обмоток генератора (по активной мощности и возбуждению), условием сохранения устойчивости его работы. Узлы со свободной реактивной мощностью также соответствуют регулируемым компенсирующим устройствам (Р=0, U = const).
Учет опорных узлов типа Р, U наиболее удобно выполнить применительно к УУН в форме баланса мощностей. Поскольку для nг узлов типа P,U реактивные мощности не заданы в уравнениях, в прямоугольной системе координат вместо соответствующих уравнений баланса реактивной мощности (8.7 6) учитываются квадратные уравнения
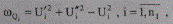(8.13)
сохраняя размерность результирующей системы (8.7).
Применительно к системе уравнений в полярных координатах (8.9) уравнения для реактивных мощностей данных типов узлов исключаются из УУН (8.9 б), а известные напряжения подставляются в остальные уравнения системы. Удобство учета заданных модулей напряжения опорных узлов (без уравнений (8.13)), снижение размерности УУН обусловило реализацию в программах расчета установившихся режимов, основанных на ньютоновских методах, преимущественно уравнений баланса мощностей (8.9). Запись уравнений в полярных координатах особенно удобна, когда заданы модули напряжении всех узлов ЭЭС. При этом система уравнений сводится к уравнениям баланса активных мощностей сети и имеет в два раза меньший размер, чем другие формы записи систем УУН [8,44,46].
Сложнее учитывать узлы данного типа применительно к УУН в форме баланса токов, поскольку реактивная мощность входит как в уравнения реактивных составляющих токов (8.6 б), (8.8 б), так и в уравнения их активных составляющих (8.6 а), (8.8 а), что видно из выражений (8.10) и (8.11), поэтому при решении систем (8.6) и (8.8) неизменной размерности условие Un = const рассматривается как дополнительное условие связи в виде (8.13). Указанная трудность учета генераторных узлов типа Р, U = const обуславливает применение методов уравнений баланса токов только для расчета сетей, не содержащих вовсе или содержащих малое количество опорных узлов [44, 46, 53]. В частности, в программах, реализующих метод Зейделя, чаще всего решаются уравнения баланса в токах (8.1), обеспечивающих простое получение соответствующих рекуррентных выражений. Выбор формы УУН и разделения переменных тесно связан с методом их решения, эффективностью соответствующих итерационных процессов, обусловлен удобством учета опорных узлов и других факторов и, в целом, требованиями, предъявляемыми к разрабатываемому программно-вычислительному аппарату.
8.1.2. Общая характеристика методов решения уравнений установившихся режимов ЭС
Выше даны математические модели установившихся режимов ЭС, использующие различные реализации УУН (8.1) — (8.2) в общем случае системы комплексных нелинейных уравнений, преобразованных к уравнениям (8.6) — (8.9), с действительными переменными (коэффициентами).
Определение напряжений U',U* или Uiδi из уравнений (8.6) — (8.9) принципиально возможно, однако нелинейность УУН не позволяет непосредственно (напрямую) решить эту задачу. Поскольку общих (точных) методов решения систем нелинейных уравнений не существует, решение системы определяется численными методами, в силу нелинейной зависимости мощности от тока и напряжения на методе последовательных приближений (итераций).
В связи с нелинейными характеристиками УУН возможны два подхода к их решению [44, 46, 47]:
1. Непосредственное решение исходных систем нелинейных УУН приближенными методами.
2. Линеаризация УУН и решение последовательности систем линеаризованных (линейных) уравнений (СЛУ) точными или приближенными методами.
Точные (прямые) методы позволяют получить истинные значения неизвестных (корни уравнений) в результате выполнения конечного числа арифметических операций, количество которых определяется только порядком системы уравнений.
Приближенные (итерационные) методы решения УУН позволяют получить истинное значение неизвестных системы лишь с заданной точностью в результате выполнения последовательности повторяющихся однотипных расчетов (итераций), число которых заранее неизвестно и зависит от скорости сходимости метода и принятых исходных приближений переменных. При этом количество арифметических операций определяется как порядком (размером) системы уравнении, так и числом итераций, за которые сходится итерационный процесс [44].
Основными требованиями, предъявляемыми к методам решения УУН на ЭВМ, является обеспечение надежности получения решений при сравнительно небольших затратах машинного времени и объема памяти [44, 46, 55].
Для более наглядной численной иллюстрации рассматриваемых ниже алгоритмов решения УУН, перепишем уравнение (8.6) — (8.9) в системе постоянного тока. Тогда имеем следующее уравнение в форме баланса токов:
(8.14)
и в форме баланса мощностей:
(8.15)
Для упрощения вычислений значения проводимостей, напряжений и задающих мощностей приняты вещественными, хотя для реальных ЭС переменного тока они являются комплексными.
Такой переход не отражается на структуре уравнений и принципиальной стороне алгоритмов, однако позволяет сократить объем вычислений, так как производятся операции не с комплексными, а с действительными уравнениями n-порядка.
Уравнения (8.14), (8.15) с действительными элементами являются точными уравнениями для ЭС постоянного тока и упрощенно описывают режим ЭС переменного тока, если сеть и нагрузки близки к однородным и падения напряжения относительно малы.
В общем случае УУН можно записать в виде системы неявных функций:
ωi (U) = 0 , i = 1,n (8.16)
Такая запись означает, что при подстановке в уравнения точного решения функции их небалансов обращаются в нуль.
В силу нелинейности УУН (8.6) — (8.9) их решение относительно переменных U при различных вычислительных схемах может быть получено только итерационно по следующему рекуррентному выражению
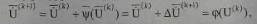(8.17)
где ψ(U(K) ) — n-мерная вектор-функция изменения переменных на k-й итерации. Способ построения ψ(U(K)) и, следовательно, получения поправок переменных ΔU(K+1) полностью определяет разновидность итерационного процесса. Суть их одна — начиная с некоторого вектора переменных U(K) , называемого начальным (исходным) приближением, изменить на величину поправок ΔU(K+1) значения его составляющих в направлении решения U(K) . При этом точное решение систем нелинейных уравнений U можно получить лишь теоретически как результат бесконечного итерационного процесса
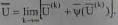
Практически решение уравнений установившихся режимов считается достигнутым, если на (k+1)-й итерации каждое уравнение сбалансировано с допустимой погрешностью η:
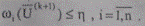(8.18)
Допустимая величина небаланса уравнений принимается, как правило, на 2-3 порядка меньше среднего значения мощностей (токов) в узлах ЭС
Указанный критерий (8.18) является наиболее строгим естественным показателем точности решения уравнений, так как при подстановке в решаемую систему уравнений точных значений неизвестных функции небалансов обращаются в нуль.
В первом приближении можно ограничиться контролем величины поправок переменных:
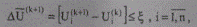(8.19)
гдеξ, — значение допустимой поправки напряжения, принимаемой в пределах (0,1—0,5)% номинального напряжения ЭС.
Естественно, что снижение допустимых значений ηи ξприводит к увеличению точности решения УУН. Вместе с тем за счет роста числа итераций увеличивается продолжительность расчетов.
Некоторые наиболее эффективные методы решения УУН рассматриваются ниже.
8.2. МОДЕЛИРОВАНИЕ И МЕТОДЫ РЕШЕНИЯ УУН
Решение систем нелинейных уравнений, описывающих установившиеся режимы, представляет центральную и наиболее трудоемкую часть алгоритмов расчета на ЭВМ параметров режима. Нахождение их решения через последовательные приближения (итерации) по формуле (8.17) может быть выполнено с помощью различных итерационных процедур, определяемых множеством способов
реализации функций ψ(UK). Для получения соответствующих рекуррентных выражений используем квадратичную часть разложения УУН (8.16) в ряд Тейлора
(8.20)
где обобщенные n-мерные векторы переменных U и поправок переменных ΔU включает компоненты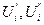 
и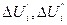 
УУН (8.6) и (8.7) в прямоугольной системе координат и компоненты Uiδi и ΔUi,Δδi УУН (8.8) и (8.9) в полярной системе координат.
Перепишем разложение (8.20) в матричном виде. Первые производные {δωj/δUj/j = 1,n } образуют i-ую вектор-строку матрицы Якоби:
Объединив все п строк,представим матрицу Якоби в виде
Вторые производные i-ro уравнения образуют матрицу Гессе:
(8.21)
С учетом приведенных матричных обозначений запишем выражение (8.20) в вида
В целом для системы УУН получим
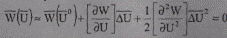, (8.22)
где W(U0 ) — вектор небалансов УУН в точке разложения U0 ; [δW/δU]— матрица Якоби, ΔU — вектор с компонентами ΔUi; [δ2W/δU2J — прямоугольная матрица Гессе, число строк в которой равно n; число столбцов — n 2 ; для каждого столбца i(j=l,n) n —столбцов определяются выражением (8.21), U2—вектор с компонентами ΔU,ΔUj, число которых равно n2.
В зависимости от числа членов разложения Тейлора и порядка производных функций небалансов, используемых для моделирования (аппроксимации) УУН и построения рекуррентного выражения итерационного процесса их решения (преобразования) (8.17), различают методы нулевого, первого и второго порядка.
Методы нулевого порядка [44, 46, 55] получаются при использовании в разложении (8.20) только нулевых (начальных) членов, не содержащих производных, что соответствует точечному представлению (точечной аппроксимации) УУН. В данном случае возможно реализовать итерационную процедуру (преобразование) (8.17) в явном виде применительно к УУН баланса токов (8.1). В практических алгоритмах наиболее часто реализуется два метода нулевого порядка: методы Зейделя и Z-матрицы.
1. Метод Z-матрицы.При заданных или известных на очередной итерации напряжениях система нелинейных УУН (8.1) становится линейной следующего вида:
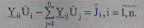
Эта же система в матричной записи
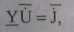(8.23)
где компоненты вектора J определяются по формуле
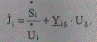(8.24)
Матричная запись УУН в виде (8.23) дает возможность реализовать процедуру (8.17) в явном виде, если воспользоваться понятием обратной матрицы и учесть свойства действий с матрицами. Для неособенной (невырожденной) матрицы коэффициентов Y (det Y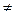 
0), являющейся матрицей узловых и взаимных проводимостей узлов, существует обратная матрица Y-1 =Zy, называемая матрицей собственных и взаимных сопротивлений узлов (Z - матрица). Умножая слева обе части системы (8.23) на Y-1, получим
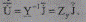
Полученные в результате решения СЛУ (8.23) напряжения U(K) следует считать исходными приближениями к искомым напряжениям UK+1 . Поэтому применительно к нелинейной системе (8.1) итерационная процедура (8.17) получения решения реализуется в виде
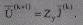(8.25)
Здесь токи j(K) в узлах уточняют на каждой итерации через напряжения предыдущей итерации U(K) по формуле (8.24). Далее по выражению (8.25) вычисляют новые приближения напряжений U(K+1) . Такой процесс продолжается до выполнения критерия (8.19).
Необходимо отметить, что матрица Zy, в отличие от матрицы Y, является заполненной, т. е. не содержит нулевых элементов и поэтому требует значительно большей, чем для матрицы Y, оперативной памяти ЭВМ для хранения ее элементов. Обращение матрицы Y осуществляется численными методами, что по своей трудоемкости эквивалентно решению систем линейных уравнений.
Метод Z-матрицы может оказаться эффективным в расчетах режимов ЭС с неизменными или малоизменяющимися конфигурацией и параметрами сети и при изменении нагрузок в узлах. В этом случае, обратив один раз матрицу Y, напряжения в узлах определяют через неизменную матрицу Z и изменяющийся в соответствии с изменением нагрузок узлов вектор правых частей УУН.
Метод Зейделя (Гаусса-Зейделя). Метод Зейделя был первым методом, примененным для расчета установившихся режимов ЭЭС на ЭВМ. Простота алгоритмической реализации, малый объем вычислений на каждом шаге, незначительная потребность оперативной памяти и приемлемая для широкого круга задач сходимость метода позволили даже на первых моделях ЭВМ рассчитывать режимы сетей, содержащих сотни узлов [46, 55, 56].
Для получения рекуррентной формулы метода необходимо непосредственно (напрямую) выразить каждое напряжение, стоящее при собственной проводимости, через другие напряжения соответствующего уравнения системы (8.1), привести уравнения к виду, удобному для итераций (нормальному виду):
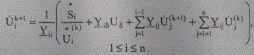(8.26)
Из формулы видно, что вместо простейшего итерационного процесса (метода Якоби), метод Зейделя использует для вычисления каждой последующей переменной самые последние (новые) значения предыдущих переменных, т. е. для вычисления текущей i-й переменной берутся значения всех предыдущих (j < i), полученных на данной (к+1) итераций, а остальные переменные Q > i) — на предыдущей (к-й) итерации. Отметим, что такая процедура вычислений значительно эффективней по сходимости, чем простая итерация.
При переходе от комплексных уравнений к действительным, выполнив в (8.26) подстановку (8.5) и выделив действительные и мнимые части, получим следующие расчетные формулы метода:
где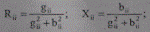 
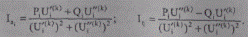
Как правило, для решения УУН применяется «ускоренный» метод Зейделя (метод релаксации). Ускорение сходимости достигается вводом в итерационную процедуру ускоряющего коэффициента (αy).
Определив обычным способом (8.27) на каждой итерации новое значение переменной Uj(k+1), вычисляется улучшенное значение Uiy(k+1) переменной:
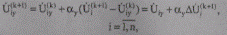(8.28)
принимаемой в качестве исходного приближения в следующей итерации.
Итерационный процесс (8.28) реализуется отдельно для продольной и поперечных составляющих напряжения:
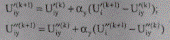(8.29)
Скорость сходимости зависит от выбранной величины αy, принимаемой в интервале 0<αу<2. Основная трудность состоит в подборе коэффициента αу, определяемого пробными расчетами. Значение αу, обеспечивающее минимальное число итераций, обычно составляет 1,2...... 1,4 [46].
Огромный опыт применения программ, основанных на методе Зейделя, показывает, что для большинства схем и нормальных эксплуатационных режимов, обеспечивается получение решения за приемлемое время. Поэтому соответствующие ПВК до сих пор применяются в службах режимов и диспетчерских управлениях электросетевых предприятий и энергосистем.
Несмотря на значительное улучшение сходимости с помощью описанного приема в ряде случаев (например, при расчете режимов сетей с повышенными нагрузками) метод Зейделя может сходиться очень медленно или даже расходиться. Поэтому, до тех пор, пока недостаточная оперативная память к быстродействие ЭВМ сдерживали применение более эффективных методов, метод Зейделя был практически основным, реализованным в промышленных программах расчета установившихся режимов ЭС.
Заметим, что нелинейность, присущая УНН баланса мощностей (8.7), (8.9), не позволяет найти решение методами нулевого порядка. Весте с тем, значительный рост возможностей ЭВМ как по быстродействию, так и оперативной памяти, повышенные требования к программам по скорости и надежности получения решения во многом стимулировали развитие и практическое применение более сложных и вместе с тем более эффективных алгоритмов, в частности, базирующихся на использовании методов первого и второго порядка. В практических алгоритмах расчета установившихся режимов ЭС используют большой класс ньютоновских и градиентных методов.
Метод Ньютона (Ньотона-Рафсона) первого порядка[44, 46, 57] является более распространенным методом решения систем нелинейных уравнений. Основное преимущество метода Ньютона выражается в быстрой и устойчивой сходимости.
Идея метода Ньютона состоит в последовательной замене на каждой итерации нелинейной системы уравнений некоторой линейной, решение которой дает значение неизвестных, более близких к решению нелинейной системы, чем исходное приближение [44, 56]. Для линейной аппроксимации УУН наряду с нулевыми элементами разложения Тейлора используются элементы первого порядка, т. е. имеем
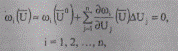(8.30)
что позволяет перейти к системе линеаризованных уравнений, например, на k-ой итерации:
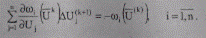(8.31)
При этом полагаем, что текущие (искомые) значения переменных U лежат в
достаточно малой окрестности ΔU = U — U(0) начальных (исходных) значении U(O)
Данный метод относится к методам первого порядка, поскольку в нем используются только первые производные, линейно аппроксимирующие УУН (8.16). Выражения производных δωi/δUj — элементов матриц СЛУ (матриц Якоби) — различны для полученных в разд. 8.1 форм записи УУН.
В результате решения СЛУ (8.31), выполняемого обычно методом Гаусса или Зейделя, определяют поправки ΔUj к предыдущим (начальным) значениям переменных. Решение системы (8.31) отражает внутренний итерационный процесс метода Ньютона. Через найденные поправки вычисляются на внешнем шаге данного метода новые (уточненные) значения переменных:
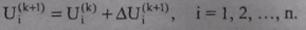(8.32)
За начальные (исходные) приближения переменных принимаются модули номинальных напряжений и нулевые значения фаз (или U' = UНОМ,U" = 0), если не известны лучшие приближения этих переменных.
В результате подстановки уточненных значении переменных и в решаемые УУН вида (8.6) — (8.9) определяются величины их небалансов. Описанная процедура повторяется до тех пор, пока не будет удовлетворен критерий (8.18), который можно реализовать в виде
(8.33)
т. е. наибольший по модулю небаланс уравнений не должен превышать заданную точность η.
Если процесс сходящийся, то решение с начального приближения достигается, как правило, за 3—4 итерации, и практически не зависит от размера системы уравнений. Об отсутствии сходимости свидетельствует большое количество итераций (более 15—20), не приводящих к решению.
Наряду с высокой сходимостью известна большая чувствительность метода Ньютона к исходному приближению переменных. Область, в пределах которой заданные исходные значения сходятся к решению, называется областью сходимости. Обычно это малая окрестность (Uk –U0 ) точки U , для которой якобиан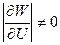 
отличен от нуля и обеспечивается высокая сходимость метода. Плохое исходное приближение переменных, т. е. взятое вне области притяжения переменных к решению, может привести к расходящемуся итерационному процессу. Алгоритм достаточно громоздок и, имея большую промежуточную информацию, требует значительного объема оперативной памяти ЭВМ.
Как видно из приведенного описания этапов алгоритма Ньютона, основной его операцией является решение СЛУ (8.31). Эффективность этой процедуры во многом определяет эффективность метода в целом.
Существует большое количество реализаций метода Ньютона и его модификаций, образующих класс ньютоновских методов. Большинство программно-вычислительных комплексов (ПВК) расчета и анализа установившихся режимов ЭЭС и систем передачи электроэнергии, разработанных в последние годы, базируются на методе Ньютона.
Метод Ньютона второго порядка [53]. Учет нелинейности при моделировании УУН осуществляется через квадратичные члены (слагаемые со вторыми производными) разложения Тейлора (8.22) в виде
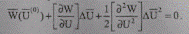(8.34)
Более полный квадратичный учет нелинейности по сравнению с линейным в методе Ньютона способствует значительно лучшей сходимости и уменьшению времени решения уравнений. Поясним это графически (рис. 8.1) на примере нелинейного уравнения с одной неизвестной ω(U).
По методу Ньютона (метод касательных), заменив в начальной точке U(0) нелинейное уравнение ω(U) касательной 1 (линейная аппроксимация) и решением линейного уравнения
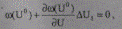
находится приращение ΔU, и значение переменной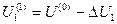 
. По методу Ньютона второго порядка нелинейное уравнение заменяется кривой второго порядка 2 (квадратичная аппроксимация) и решением квадратичного уравнения
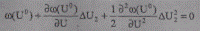(8.34 а)
вычисляется приращение ΔU2, дающее новое значение переменной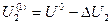 
, которое значительно ближе к точному решению (корню) U по сравнению с приближением 
, полученным методом Ньютона.
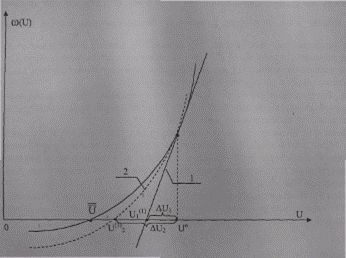
Рис. 8.1. Линейная (1) и квадратичная (2) аппроксимации нелинейного уравнения ω(U) в точке U(0).
Приращение ΔU2, определяемое из решения квадратичного уравнения (8.34 а), назовем приращением второго порядка. Использование его в рекуррентном выражении итерационного процесса при определенных условиях обеспечивает более быструю и надежную сходимость.
Возвращаемся к общему (многомерному) случаю. Основная трудность метода второго порядка заключается в решении системы (8.22) квадратичных уравнений (СКУ)
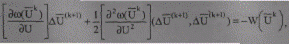(8.35)
на каждом шаге вместо СЛУ (8.31)
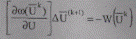(8.36)
в методе Ньютона первого порядка.
Существуют различные пути алгоритмической реализации метода второго порядка в зависимости от способа получения приращения ΔU из СКУ (8.35). В связи с тем, что применение прямых методов для этой цели невозможно, учет нелинейности УУН посредством квадратичного разложения осуществляется косвенно и связан с дополнительным решением СЛУ в новом итерационном процессе.
Обозначим ΔU, как вектор приращения первого порядка, полученный методом Ньютона при решении СЛУ (8.36). Используя ΔU1, результирующее приращение второго порядка можно определить из решения вспомогательной СЛУ
