ГЛАВА 5. РЕЖИМНЫЕ ПОКАЗАТЕЛИ УЧАСТКА ЭЛЕКТРИЧЕСКОЙ СЕТИ

5.1. ОБЩАЯ ХАРАКТЕРИСТИКА ЗАДАЧИ РАСЧЕТА И АНАЛИЗА УСТАНОВИВШИХСЯ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ

Передача электроэнергии от электростанций к потребителям осуществляет­ся по электрическим сетям. В теории и практике электроэнергетических (электри­ческих) систем (ЭЭС) термин «электрическая сеть», с одной стороны, соответст­вует понятию подсистемы ЭЭС, предназначенной для передачи и распределения электроэнергии, как совокупности ЛЭП и подстанций, соединяющих между собой источники питания (ИП) и электропотребители (ЭП). С другой стороны, это элек­трическая цепь, соответствующая данной подсистеме. Естественно, такая элек­трическая цепь обязательно включает в себя ИП и ЭП как составные части, и в едином смысле понятие электрической сети формально совпадает с понятием ЭЭС как электрической цепи [5, 8]. В зависимости от величины мощности и вида электропотребителей, удаленности их от электростанций, передача и распределе­ние электроэнергии осуществляется по сетям различных номинальных напряже­ний и конфигураций. Моделирование, расчет и анализ параметров электрических сетей и нагрузок (потребителей) рассмотрены в главах 2—4.

При решении ряда задач эксплуатации, развития и проектирования электри­ческих сетей необходимо оценить условия, в которых будут работать потребители и оборудование электрической сети. Также эти оценки дают возможность устано­вить допустимость анализируемого режима при передаче по сети данных мощно­стей, при подключении новых и отключении действующих элементов сети (ЛЭП, трансформаторов, нагрузок и т. д.). Кроме того, расчеты, выполняемые при такого рода оценках, дают возможность предусмотреть меры для обеспечения требуемо­го качества электроэнергии и определить условия для оптимизации производства, передачи и распределения электроэнергии.

Плановые и аварийные изменения нагрузок, состава и конфигурации схемы электрической сети приводят к изменению ее электрического режима. Определе­ние параметров рабочего установившегося режима (состояния электрического равновесия) электрической сети (тока и потокораспределения, напряжений и по­терь мощности в сети) составляет задачу расчета режима или, как иногда условно говорят, задачу «электрического расчета» сети.

Расчет и анализ параметров установившихся режимов составляют основную задачу при проектировании ЭЭС с учетом надежности эксплуатации и экономи­ческих факторов.

В общем случае рабочие режимы электрических сетей являются несиммет­ричными и несинусоидальными. Симметричный синусоидальный режим следует рассматривать как частный случай. Однако если степень несимметрии и несину­соидальности кривых токов и напряжений относительно невелика, что достаточно часто имеет место, то в этом случае режим рассматривается как симметричный и синусоидальный, что позволяет значительно облегчить его расчет.

Расчет режима сети в общем случае представляет собой весьма сложную задачу. Это связано как с большим количеством элементов, образующих сети со­временных электрических систем, так и со специфическими особенностями зада­ния исходных данных.

Исходными данными для расчета установившихся режимов служат: схема электрических соединений и параметры сети электроэнергетической системы, дан­ные о потребителях (нагрузках) и источниках электроэнергии (электростанциях).

Нагрузки реальных электрических сетей при их проектировании и эксплуата­ции обычно задают значениями потребляемых ими активных и реактивных мощно­стей (Р_i + jQ_i = S_j) или токов (I_i, cosφ), которые могут приниматься постоянными, ли­бо зависящими от напряжения в точке подключения нагрузки в сети, т. е.

Исходными данными об источниках питания, как правило, служат выдавае­мые генераторами в сеть активные мощности (P_i = const) и модули напряжений в точках подключения (U_i = const); в ряде случаев источники питания могут быть за­даны и постоянными значениями активных и реактивных мощностей (Р_i = const, Q_i = const), аналогично нагрузкам. Кроме того, один из источников (как правило, наиболее мощная электростанция), играющий роль балансирующего, задается комплексным значением напряжения (U_δ = const).

Электрическая сеть ЭЭС представляется схемой замещения, параметры ко­торой обычно разделяют на продольные, входящие в последовательную цепь пе­редачи и распределения электроэнергии (сопротивления ЛЭП и трансформаторов и др.) и поперечные, соответствующие шунтам схемы (проводимости ЛЭП, трансформаторов, нагрузок).

При анализе режимов ЭЭС продольные параметры ЛЭП с проводами из цвет­ного металла (активные и реактивные сопротивления) и поперечные параметры (ак­тивные и реактивные проводимости) принимают постоянными, не зависящими от параметров электрического режима. При рассмотрении ВЛ со стальными проводами необходимо учитывать нелинейность их параметров от токов нагрузки.

^ Симметричные установившиеся режимы работы трехфазных электрических сетей характеризуются одинаковыми значениями параметров режима отдельных фаз и синусоидальной формой кривых тока и напряжений. В этих условиях значе­ние полной мощности для трехфазной цепи («трехфазная мощность») определяет­ся комплексным числом.

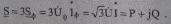(5.1)

Наибольшую нелинейность в аналитическое содержание задачи вносят электрические нагрузки узлов ЭЭС. При расчете установившихся режимов ЭЭС нагрузки узлов (электропотребители и источники питания) задаются в общем случае их неизменными мощностями или зависимостями этих мощностей от искомых параметров режима (напряжения, угла выбега ротора синхронных машин и т. п.), так называемыми статическими характеристиками.

Если нагрузки узлов электрической сети учитываются значениями требуе­мой активной и реактивной мощности, то ток каждой фазы нагрузки может быть вычислен только при известном напряжении U; на зажимах этой нагрузки, вы­числяемом в ходе расчета напряжений и фазных токов:¹

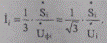(5.2)

'Переход к междуфазному напряжению выполнен с допущением одинаковости угла сдвига фазного и междуфазного напряжений, что сделано в целях получения минимально уп­рощенного выражения мощности через междуфазное напряжение, которое опережает по фазе фазное напряжение соответствующей фазы на 30°. При анализе установившихся режимов элек­трических сетей это допущение значения не имеет. Однако в некоторых других случаях необ­ходимо иметь в виду, что в (4.2) комплекс тока нагрузки или генератора имеет аргумент, сме­щенный на 30° по отношению к действительному аргументу тока в линейных проводах [5, 29].

Это обстоятельство препятствует непосредственному использованию законов Кирхгофа для получения однозначного решения. В этом заключается основное отличие анализа установившихся режимов ЭЭС от классического анализа элек­трических цепей, где источники питания и электропотребители представляются в виде источников ЭДС и источников тока с соответствующими сопротивлениями.

Такой подход к анализу ЭЭС объясняется тем, что здесь основное значение имеют энергетические характеристики, и они являются определяющими для ре­жима систем. Вместе с тем анализ этих режимов, естественно, можно вести также непосредственно на основе алгоритмов классической теории электрических цепей с соответствующим пересчетом мощностей через токи и напряжения.

Расчеты параметров установившихся режимов обычно выполняют автома­тически формализованными методами с помощью ЭВМ [44—48, 55-57]. Матема­тически задача сводится к решению системы нелинейных уравнений из-за нели­нейной зависимости мощности от тока и напряжения. Наиболее часто установив­шиеся режимы ЭЭС описываются уравнениями узловых напряжений, представ­ляемых в форме баланса токов:

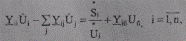(5.3)

или в форме баланса мощностей

(5.4)

Разработан большой класс методов решения этих уравнений [44-48,53,55-59] Инженерная оценка параметров установившихся режимов при изучении процессов проектирования и эксплуатации ЭЭС может выполняться традицион­ными методами, реализуемыми вручную. Эти методы базируются главным образом на прямом использовании основных законов электрических цепей (Кирхгофа, Ома и Джоуля-Ленца) и методов их эквивалентных преобразований с широкой интерпретацией соотношений между параметрами режима с помощью векторных и круговых диаграмм [5, 8, 11, 24, 29, 49, 72, 77].

Весьма ценным свойством традиционных методов является их большая на­глядность, простота толкований сущности электрических режимов, благодаря че­му они широко применяются и в настоящее время. Кроме того, они имеют важное учебно-методическое значение, поскольку подготавливают студентов к переходу к более совершенным и универсальным современным методам анализа электри­ческих режимов.

Ниже рассматриваются некоторые положения теории, наиболее используе­мые соотношения, реализуемые в традиционных инженерных методах расчета с применением числовых примеров для простых электрических сетей.

5.2. АНАЛИЗ РЕЖИМА НАПРЯЖЕНИЙ УЧАСТКА ЭЛЕКТРИЧЕСКОЙ СЕТИ

Рассмотрим участок (звено) электрической сети, под которым следует по­нимать участок ее схемы замещения, состоящий из одной продольной ветви с со­противлением Z = R + jX; например, линии электропередачи или трансформатора

(рис. 5.1).

Рис. 5.1. Схема замещения фазы участка сети

Этот участок питает симметричную трехфазную электрическую нагрузку, заданную в конце участка полным током I или мощностью трех фаз («трехфазной мощностью») S₂, которые потребляются сопротивлениями R_н,,Х_н нагрузки (на рис. 5.1 они показаны штриховыми линиями). На рис. 5.1 и в дальнейшем все парамет­ры, относящиеся к началу участка (питающий конец схемы), отмечены индексом 1 или Н, а параметры, относящиеся к концу участка (приемный конец схемы) — индексом 2 или К.

При одинаковой нагрузке и сопротивлениях фаз токи в проводах (обмотках) участка будут равны по величине и иметь одинаковый сдвиг по фазе:

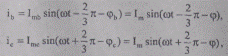(5.5)

относительно соответствующих фазных напряжений в конце участка (индекс 2 для упрощения записи опущен):

(5.6)

В дальнейшем модули вращающихся векторов тока и напряжения прини­маются равными действующим значениям U = U_m/√2, I = I_m/√2 вместо ам­плитудных.

Рис. 5.2. Векторное изображение напряжения и тока

Ввиду того, что синусоидальные величины тока и напряжения в синхронно работающих ЭЭС изменяются с одинаковой частотой ω = 2πf, фазовые углы век­торов задаются в один момент времени (например, на рис. 5.2 для напряжения U фазовый угол будет δ, для тока I — фазовый угол φ).

При расчетах симметричных рабочих режимов трехфазных сетей достаточ­но рассмотреть только одну фазу участка, т. е. анализировать токи и фазные на­пряжения для одной фазы, так как токи и напряжения других фаз имеют те же значения, но со сдвигом на 2/3πрад. Далее можно перейти к линейным напряже­ниям.

Обращаемся к схеме замещения участка. Вектор напряжения в конце линии U_2ф = U_2фе^jδ совместим с действительной осью. В этом случае δ = 0 и U_2ф = U_2ф

При неизменной мощности нагрузки S₂ = Р₂ + jQ₂, определим ток в фазном проводе линии

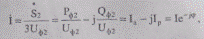(5.7)

отстающий на угол φ от фазного напряжения (активно-индуктивная нагрузка), т. е. допустим, что известны U_2ф, I и φ, и необходимо определить U_1ф, и угол δ меж­ду векторами U_{1ф |} и U_2ф. Расчет можно вести по току I и по мощности нагрузки S₂.

В соответствии с законом Ома для участка цепи применительно к фазным напряжениям запишем:

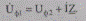(5.8)

Между напряжениями в начале U_1ф и конце U_2ф участка 1—2 (рис. 5.1) существует некоторая разность как по величине, так и по фазе.

Величина

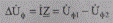(5.9)

является падением напряжения и определяется разностью комплексных дейст­вующих значений фазных напряжений начала и конца участка сети. Заменив в (5.9) комплексные величины I и Z на действительные и мнимые составляющие, получим

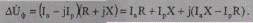(5.10)

Представим вектор ΔU_ф в виде составляющих.

Продольная (по направлению U_2ф) составляющая падения напряжения в линии

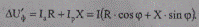(5.11)

Поперечная (перпендикулярная к направлению U_2ф) составляющая падения напряжения в линии

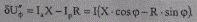(5.12)

Зная составляющие падения напряжения, можно определить, в соответствии с выражением (5.8), вектор напряжения в начале участка:

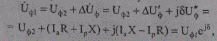(5.13)

где модуль этого напряжения

(5.14)

и его фаза

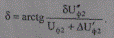(4.15)

Перепишем закон Ома для участка электрической сети (5.9) в следующем виде:

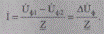(5.16)

Величину

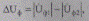(5.17)

определяемую разностью модулей напряжений начала и конца участка, называют потерей напряжения.

Полученные выше выражения, характеризующие режим участка сети, ото­бразим геометрически с помощью векторной диаграммы фазных напряжений и токов (рис. 5.3). Построение начинаем от центра координат, откладывая по оси действительных величин вектор напряжения U_2ф, и отстающий от него на угол φ вектор тока I. С конца вектора U_2ф откладываем параллельно вектору тока I век­тор падения напряжения IR в активном сопротивлении. Вектор падения напряже­ния на индуктивном сопротивлении jIX направлен перпендикулярно вектору то­ка. Сумма этих векторов образует вектор падения напряжения ΔU_ф. Таким обра­зом получим треугольник падения напряжения abc. Соединив начало координат о и вершину с треугольника падения напряжения, получим вектор фазного напря­жения U_1ф, в начале участка (вектор ос), опережающий вектор U_2ф на угол δ. Век­тор напряжения U_1ф в начале участка образуется геометрическим суммированием векторов U_2ф и ΔU_ф. Из векторной диаграммы видно, что падение напряжения ΔU_ф (вектор ас) — это геометрическая разность между векторами напряжения начала U_1ф и конца U_2ф участка.

Потери напряжения — это алгебраическая разность модулей напряжений по концам участка, соответствует отрезку af (точка f получена в результате пересе­чения оси действительных величин с другой, проведенной радиусом ос U_1ф).

Аналитические выражения составляющих падение напряжения (5.11) и (5.12) можно получить также из геометрических соотношений векторной диа­граммы (рис. 5.3). Для продольной составляющей получим

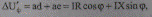(5.18)

для поперечной составляющей

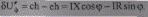(5.19)

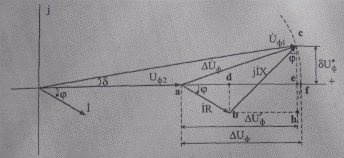
Рис. 5.3. Векторная диаграмма напряжений и тока фазы участка электрической сети

Для выполнения электрических расчетов удобнее применять линейные (межфазные) напряжения и «трехфазные» мощности. Для того чтобы перейти к этим величинам, умножим обе части формулы (5.13) на √3 и запишем в виде

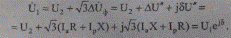(5.20)

Аналогично, учитывая соотношение между линейными и фазными напря­жениями

U=√3U_ф, закон Ома (4.8) можно записать следующим образом:

(5.21)

Поскольку участок сети состоит только из продольного сопротивления (рис. 5.1), ток в начале и конце звена остается неизменным.

Следует обратить внимание на то, что указанное вычисление междуфазных напряжений является условным. При этом правильно определяются только мо­дуль линейных напряжений, а их аргументы (фазы) условно принимаются такими же, как и для фазных значений напряжений. Для расчетов рабочих режимов элек­трических сетей принятое допущение не имеет значения. Однако это следует иметь в виду в тех случаях, когда необходимо знать действительные значения ар­гументов для линейных напряжений [29]. Вектор линейного напряжения опере­жает вектор U_ф соответствующей фазы на 30°.

В результате замены в (5.20) согласно (5.2) токов через параметры конца участка

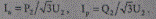(5.22)

Можно записать выражение (5.20), связывающее напряжения начала U₁ и конца U₂ участка, в следующем виде:

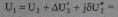
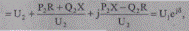(5.23)

где модуль (величина) линейного напряжения

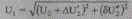(5.24)

и его фаза (с учетом вышеприведенного замечания)

(5.25)

вычисляются по аналогичным выражениям (5.14) и (5.15) с фазными составляю­щими.

Влияние поперечной составляющей на модуль напряжения можно учесть приближенно [11, 29]:

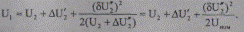(5.26)

Если известны напряжение U, и мощность S, начала участка, то можно оп­ределить напряжение конца участка следующим образом:

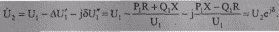(5.27)

Величина (модуль) напряжения определяется точным выражением

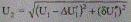(5.28)

или приближенно по формуле

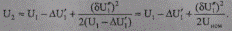(5.29)

Отметим, что формулы (5.26) и (5.29) дают высокую степень точности оп­ределения U₁ и U₂, и поэтому могут применяться во всех инженерных расчетах се­тей [11].

Значение фазы находится в виде

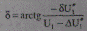(5.30)

и по модулю равно величине (5.25), определяемой через параметры конца участка.

Для наглядности анализа напряжений выделим из векторной диаграммы на рис. 5.3 фрагмент, иллюстрирующий связь напряжений начала и конца участка (рис. 5.4). Здесь показан отдельно треугольник падений напряжений на комплекс­ном сопротивлении Z, вычисленный через параметры S₂, U₂ конца участка:

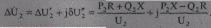(5.31)

Дополним его треугольником падения напряжения (показан на рис. 5.4 пунктиром), вычисленный через параметры S₁, U₁ начала участка:

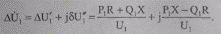(5.32)

Необходимо отметить, что векторы падения напряжения ΔU₁ и ΔU₂ ориен­тированы относительно различных векторов напряжения: ΔU₁ относительно на­пряжения в начале, а ΔU₂, относительно напряжения в конце участка. Поэтому соответствующие одноименные составляющие падения напряжения, вычислен­ные по данным начала и конца участка, не равны друг другу, т. е.

(5.33)

(5.34)

при равенстве модулей анализируемых падений напряжений (5.31) и (5.32)

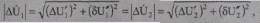(5.35)

вычисленных по данным начала и конца участка.

Отмеченное видно на векторных диаграммах (рис. 5.4), построенных по вы­ражениям (5.23) и (5.27).

В общем случае в соответствии с законом Ома для участка сети примени­тельно к междуфазным напряжениям

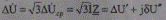(5.36)

компоненты вектора падения напряжения, аналогично (5.11) и (5.12), находят в виде

.

(5.37)

где активную и реактивную составляющие тока вычисляют по выражению (5.2) через данные в начале или в конце звена.

Обратимся к графическому представлению (интерпретации) состояния на­пряжений. При анализе режима по данным конца звена (U₂,P₂,Q₂) вектор напря­жения U₂ откладываем от начала координат в направлении оси действительных величин + (рис. 5.4), т. е. приравниваем его модулю. От конца вектора U₂ в том же направлении откладываем продольную составляющую падения напряжения ΔU^’₂ а перпендикулярно ей — вектор поперечной составляющей δU^’’₂. Суммирование обеих составляющих образует треугольник падения напряжения, гипотенуза ко­торого является модулем падения напряжения. При расчетах по данным начала участка (U_1,P₁,Q₁,) действительная ось +' совмещается с вектором U₁ (рис. 5.4), тем самым координатные оси, поворачиваясь против часовой стрелки на угол δ, l принимают новое положение +', j' в пространстве которых нужно от конца вектора U₁ отложить в обратном направлении (вычесть) продольную составляющую падения напряжения ΔU’₁, а затем перпендикулярно ему — поперечную состав­ляющую падения напряжения δU^’’₁, сумма которых даст вектор ΔU₁, (рис. 5.4, пунктирные линии). Соединив конец вектора δU’’₁ с началом координат, получим вектор напряжения U₂ в конце звена.

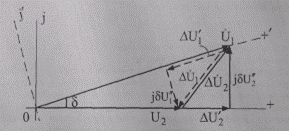
Рис. 5.4. Векторная диаграмма напряжений участка сети

Такое построение диаграмм напряжений с выделением треугольников паде­ния напряжения отражает влияние отдельных составляющих комплексного со­противления Z участка и комплексной мощности S (тока I). Из векторной диа­граммы следует, что при заданных активной Р и реактивной Q мощностях в конце участка поперечная составляющая падения напряжения δU^’’ тем больше, чем больше реактивное сопротивление участка X его активного сопротивления R и, следовательно, тем больше угол сдвига δ между векторами напряжений U₁ и U₂.

Как известно, для линий напряжением 110 кВ и выше (см. ч. 1, рис. 2.2) и всех силовых трансформаторов X > R, причем для ЛЭП напряжением 220 кВ и выше, а также трансформаторов мощностью более 4 МВА X » R. Поэтому при значительных длинах таких линий или при работе сетей, содержащих эти элемен­ты, с нагрузками, близкими к проектным, значения углов сдвига δ становятся большими, как правило, около 15—25°, с увеличением δ до 35—55° при увели­ченной протяженности ЛЭП или передаче мощностей, близких к нормативным по статической устойчивости. В этих случаях учет поперечной составляющей δU'' вносит уточнения в расчеты напряжения, существенно превышающие погрешно­сти информации о параметрах сети, а потому анализ электрических режимов дол­жен выполняться с учетом поперечной составляющей падения напряжения. И, на­оборот, для участков напряжением 110 кВ и менее X ≤ R угол δ небольшой (ме­нее 2—3°). В этом случае с достаточной точностью (ошибка менее 0,5 %) можно считать, что падение напряжения равно его продольной составляющей ΔU'. Тогда формулы (5.23) и (5.27) упрощаются и приобретают вид

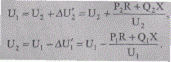(5.38)

Такое упрощение вносит ошибку не более долей процента, а потеря напря­жения приближенно определяется по формуле

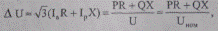(5.39)

где мощность и напряжение соответствуют одному и тому же узлу или подстав­ляется номинальное напряжение участка.

По векторной диаграмме рис. 5.4, с учетом выражений (5.31) и (5.32), мож­но установить влияние составляющих активной и реактивной мощностей (тока) участка или изменение его коэффициента мощности cosφ на падение и потерю напряжения при заданных значениях сопротивлений R и X. Видно, что при задан­ной (неизменной) активной мощности нагрузки и возрастании реактивной мощ­ности Q (тока I_р) прямо пропорционально увеличивается продольная составляю­щая падения напряжения ΔU' и уменьшается ее поперечная составляющая δU’’ (при δ>0 выполняется в большинстве случаев). В результате возрастают падение и потери напряжения, угол сдвига δ уменьшается. И, наоборот, увеличение коэф­фициента мощности нагрузки cosφ₂ уменьшает передаваемую по звену реактив­ную мощность Q₂, а следовательно, и снижает падение и потерю напряжения на участке сети.

Характер нагрузки влияет на изменение напряжений в начале и конце звена. На рис. 5.5 приведены векторные диаграммы фазных напряжений и токов участка сети с активно-индуктивным сопротивлением для активной (рис. 5.5, а), индук­тивной (рис. 5.5, б) и емкостной (рис. 5.5, в) нагрузки I. Анализ данных частных случаев позволяет установить граничные состояния напряжений участка реальной сети, в пределах которых находятся наиболее распространенные общие случаи за­грузки сети. Так, например, при активно-индуктивной нагрузке во всех случаях (при изменении cosφ от 1 до 0) напряжение U₁ в начале участка больше напря­жения U₂ в конце, а вектор напряжения U₂ преобразуется из отстающего (δ<0) по отношению к вектору U₁ в опережающий (δ>0). При активно-емкостной на­грузке вектор напряжения U₁ в начале участка всегда опережает вектор напряже­ния U₂ в конце участка, а модуль напряжения U₂ увеличивается (по мере при­ближения cosφ к 0) от значений U₂< U₁ до величины U₂>U₁.

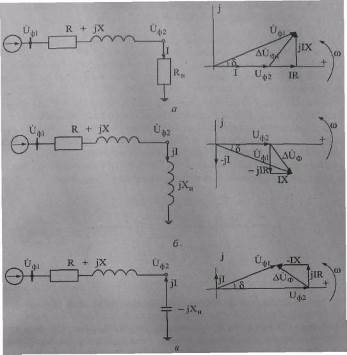
Рис. 5.5. Векторные диаграммы напряжений и токов участка сети для активной (а), индуктивной (б) и емкостной (в) нагрузки I

Более тщательный анализ напряжений можно выполнить с помощью ЭВМ при неизменном модуле нагрузки (I_H= const) и переменном ее составе (cos φ_н— var) [46, 50] или используя круговые диаграммы зависимостей мощности от вели­чины и фазы напряжений [5, 8, 11].

5.3. РАСЧЕТ И АНАЛИЗ УСТАНОВИВШЕГОСЯ РЕЖИМА УЧАСТКА ЭЛЕКТРИЧЕСКОЙ СЕТИ

В качестве участка может рассматриваться любой элемент трехфазной элек­трической сети (линия электропередачи, трансформатор и т.д.), в дальнейшем именуемый также общим термином — электропередача. Предварительно рас­смотрим участок — электропередачу, схема замещения которого состоит из одной продольной ветви с сопротивлением

Z = R + jX (рис. 5.6).

Характеристика участка и его нагрузки дана в параграфе 5.2. Для энергети­ческой характеристики работы электропередачи используем значения активной и реактивной мощности, предполагая их известными в начале S₁= P₁ + jQ₁,, или в конце S₂ = P₂ + jQ₂ электропередачи. Другими словами, известны комплексные значения полной мощности трех фаз («трехфазная мощность») у передающего S₁ и приемного S₂ конца электропередачи. Для однозначности анализа полагаем также известными напряжения в начале U₁ и в конце U₂ участка.

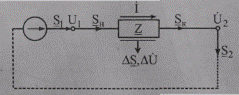
Рис. 5.6. Схема замещения участка сети с обозначением потоков мощности

В данном элементарном случае участок сети не содержит поперечных вет­вей — шунтов, поэтому ток в начале и конце звена неизменный по величине и по фазе, а мощность источника (генерация) равна потоку мощности в начале звена (S₁= S_н, так же как и мощность электропотребителя (нагрузки) равна мощности в конце звена (S₂ = S_к)

(рис. 5.6). Однако мощности по концам участка при 1≠0 раз­личаются на величину разности комплексов (векторов):

(5.40)

называемой потерей мощности. Причем это различие тем заметнее, чем больше модуль (абсолютная величина) падения напряжения:

именуемый потерей напряжения. Характеристика и вычисление показателей, определяющих режим напряжения, приведены в параграфе 5.2. Расчет и анализ взаимосвязи мощностей и напряжений по концам участка посредством показателей ΔS и ΔU и определяет способ (характер процесса) расчета его электрического режима. Рассмотрим наиболее характерные для практики случаи расчета.

Расчет по данным, характеризующим начало участка. Известны мощ­ность и напряжение в начале участка S₁ и U₁; требуется определить мощность и напряжение в конце участка S₂ и U₂. На практике этот случай имеет место тогда, когда возникает необходимость передачи заданной мощности источника (элек­тростанции), при фиксированном напряжении на его шинах, в приемную систему или узел потребления. При этом следует определить, каковы будут затраты (поте­ри) мощности и напряжения на приемном конце электропередачи. Полагаем, что нагрузка имеет активно-индуктивный характер (ток звена I отстает от напряже­ния U₁ на угол φ). Тогда комплексное значение полной мощности в начале участ­ка будет

(5.41)

Откуда комплексное значение полного тока

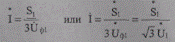(5.42)

и значения его составляющих

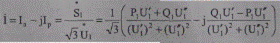(5.43)

вычисляют точно через известные мощность S₁ и напряжение U₁ в начальном уз­ле схемы. По этой же причине имеется возможность точно вычислить зависящие от тока потери мощности ΔS и падение напряжения ΔU, а потому расчет режима участка выполняется в один этап от начала к концу звена, т. е. реализуется прямая (точная) процедура расчета.

Коэффициент мощности в начале ветви

(5.44)

Предположим, что известно напряжение U_ф1 (его замер) в начале звена. То­гда при известной мощности S₁ можно точно определить ток ветви в виде

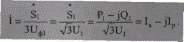(5.45)

При протекании тока I по участку с сопротивлением Z происходит потеря активной и реактивной мощностей, которые в соответствии с законом Джоуля-Ленца запишем через составляющие тока:

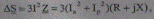(5.46)

или, пользуясь значениями активной и реактивной мощности, в соответствии с (5.45) запишем

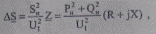(5.47)

откуда потери активной и реактивной мощности

(5.48)

Множитель «3» исчез, поскольку выполнена подстановка модуля тока, вы­численного через линейное напряжение U = √3U_ф.

Поток мощности в конце ветви меньше на величину потерь

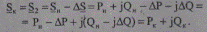(5.49)

Ток в продольном участке сети наряду с потерями мощности вызывает па­дение напряжения (см. параграф 5.2):

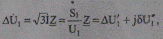
на величину которого (в соответствии с указанным направлением тока) напряже­ние в конце участка меньше напряжения в начале

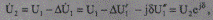(5.50)

где модуль и фаза напряжения приемного конца электропередачи определяются по формулам (5.28) и (5.30). Составляющие вектора падения напряжения ΔU₁ можно найти по выражениям, использующим ток (5.37) или мощность начала участка (5.32).

Режим напряжения данного участка сети можно характеризовать с помо­щью векторной диаграммы (рис. 5.4.), построенной в координатных осях +, j.

С учетом найденного напряжения U₂ мощность в конце звена (5.49) можно также записать в виде

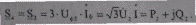(5.51)

Откуда с учетом (5.42) получим очень важное выражение для тока звена

(5.52)

или в записи через линейные напряжения (с учетом отмеченного на с. 6 допущения) имеем

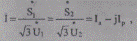(5.53)

т. е. ток можно вычислить по данным начала или конца звена.

Таким образом, ток участка сети можно вычислить через мощность и на­пряжение в начале или конце звена.

Рабочий режим участка сети можно характеризовать распределением пол­ной мощности по участку (рис. 5.6.) и соответствующей векторной диаграммой (рис. 5.7), отражающей связь мощностей начала, конца участка и потерь в нем по­средством балансового соотношения (5.49).

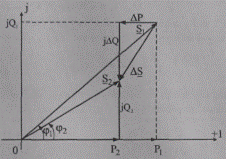
Рис. 5.7. Векторная диаграмма мощности для участка сети

В соответствии с последним из исходного вектора мощности начала участка S₁, откладывая параллельно оси абсцисс, вычитаем вектор потерь активной мощ­ности ΔР. С конца вектора ΔР, откладывая параллельно оси ординат, вычитаем вектор потерь реактивной мощности ΔQ. В итоге полученный вектор ΔS вычита­ем из вектора S₁. Соединив конец вектора ΔS с началом координат, получим век­тор мощности S₂ в конце участка с составляющими Р₂ и Q₂ (рис. 5.7). Углы накло­на φ₁ и φ ₂ векторов мощности S₁ и S₂ к оси вещественных величин определяют значения коэффициента мощности. В частности, в конце участка имеем

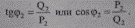(5.54)

Коэффициент полезного действия участка сети в процентах

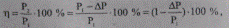(5.55)

т. е. снижение потерь активной мощности увеличивает КПД электрической сети.

Расчет режима по данным, характеризующим конец участка.Полагаем известными мощность и напряжение в конце участка S₂ и U₂. S₂=const, U₂=const. Требуется определить мощность S₁ и напряжение U₁ в начале участка. Этот случай встречается на практике тогда, когда, например, задана нагрузка потреби­теля и необходимо определить напряжение U₁ источника питания, при котором будет обеспечено требуемое напряжение U₂ у потребителя. При этом также вы­ясняется, каковы затраты (потери) мощности на передачу электропотребителю необходимой мощности.

В общем случае принимаем, что заданная электрическая нагрузка в узле 2 активно-индуктивная:

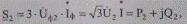(5.56)

и поскольку ток I звена неизменен и равен току нагрузки, его значение вычисля­ют точно через заданные мощности S2и напряжение U₂ в конечном узле схемы:

(5.57)

где составляющие комплексного полного тока можно выразить аналогично (5.43) через составляющие мощности S₂= Р₂ + jQ₂ и напряжения U₂ = U'₂ + jU₂^’’ в сле­дующем виде:

(5.58)

Поскольку напряжение в узле задается, как правило, вещественным моду­лем U₂ (например, в результате измерения напряжения), то выражение для тока (5.57) примет следующий частный вид:

(5.59)

Точность вычисления тока звена, как и в предыдущем случае, определяет прямой характер расчета, в один этап от конца к началу участка.

Теперь потери мощности можно определить следующим образом:

или через известные составляющие мощности

(5.60)

Откуда потери активной и реактивной мощности

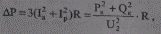
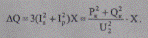(5.61)

Падение напряжения на участке сети

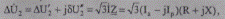(5.62)

или через известные составляющие мощности

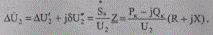(5.63)

Откуда продольная и поперечная составляющие вектора падения напряже­ния, ориентированные относительно вектора напряжения U₂ конца участка, вы­числяются по формулам (5.37) или (5.31).

В соответствии с известным направлением потока (тока) от начала к концу звена (рис. 5.6) мощность в начале звена S_н больше мощности в конце S_к, на вели­чину потерь ΔS:

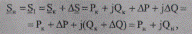(5.64)

а напряжение в начале звена U₁ больше напряжения в конце на величину падения Д U

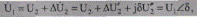
где модуль и фазу напряжения передающего конца электропередачи вычисляют по формулам (5.24) и (5.25).

С учетом найденного напряжения U, мощность в начале звена можно выра­зить в виде

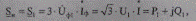
откуда с учетом (5.57) получим

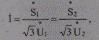
т. е., как и в предыдущем случае, ток звена можно вычислить как по данным на­чала, так и по данным конца звена.

Векторная диаграмма напряжения, интерпретирующая электрическое со­стояние звена, для данного случая приведена на рис. 5.4.