Теорема умножения вероятностей.

Перед тем как излагать теорему умножения вероятностей, введём ещё одно важное понятие: понятие о независимых и зависимых событиях.

Событие А называется независимым от события В, если вероятность события А не зависит от того , произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Рассмотрим примеры:

Опыт состоит в бросании 2-х монет, рассматриваются события:

А - появление герба на второй монете,

В - появление герба на первой монете

В данном случае вероятность события А не зависит от того, произошло событие В или нет. Событие А не зависимо от события В.

В урне два белых шара и один чёрный. Два лица вынимают из урны по одному шару; рассматриваются события:

А - появление белого шара у 2-го лица;

В - появление белого шара у 1-го лица.

Вероятность события А до того, как известно что-либо о событии В равна 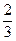. Если стало известно, что событие В произошло, то вероятность события А становится рав ной 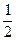, из чего заключаем, что события А зависит от события В.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается .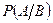

Для условия последнего примера

и если мы введём в рассмотрение событие С - появление у 1-го лица чёрного шара .

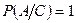Условие независимости события А от события В можно записать в виде

.

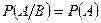а условие зависимости - в виде

.

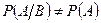Перейдем к формулировке и доказательству теоремы умножения вероятности. Теорема умножения вероятностей формулируется следующим образом : Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

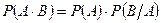
Докажем теорему умножения для схемы случаев .Пусть в урне имеется n шаров, из них m шаров красных, а k шаров с рисунком, из них l шаров-красных. Найти вероятность того, что мы вынем красный шар с рисунком. Изобразим этот опыт для наглядности на рисунке:

Где n-число всех случаев

m - число случаев,благоприятствующих событиюА(красные шары)

k - число случаев,благоприятствующих событию

(красных шаров с рисунком)

вычислим то есть условную вероятность события B в предложении , что A имело место .Если известно ,что событие A произошло то из ранее возможных случаев остаются возможными только те которые благоприятствовали событию A.Из них l случаев благоприятны событию B.

Следовательно

Теорема доказана.Очевидно что применение теоремы умножения вполне безразлично,какое из событий A и B считать первым а какое вторым и теорему умножения записать и в каком виде

Частный случай

Если A и B события независимые ,то условная вероятность

И следовательно

Обобщение для и независимых событий

Или

П- знак произведения .

Прибор состоит из трех узлов.

Надежность узлов представлена на рисунке

Найти надежность всего прибора