Уравнения Колмогорова. Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем на примере случайного процесса из предыдущего примера, граф которого изображен на рис. 15. Будем полагать, что все переходы системы из состояния S_i в S_j происходят под воздействием простейших потоков событий с интенсивностями 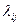(i, j = 0, 1, 2, 3); так, переход системы из состояния S₀ в S₁ будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния S₁ в S₀ — под воздействием потока окончаний ремонтов первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 3.1). Рассматриваемая система S имеет четыре возможных состояния: S₀ ,S₁ , S₂ , S₃.

Вероятностью i-го состояния называется вероятность p_i(t) того, что в момент t система будет находиться в состоянии S,. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице:

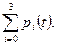(3.1)

Система дифференциальных уравнений Колмогорова для вероятностей состояний:

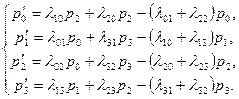(3.2.)

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (1-го состояния).

В системе (3.2) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (3.1).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент t = 0. Так, например, систему уравнений (15.9) естественно решать при условии, что в начальный момент обе бригады свободны и система находилась в состоянии S₀, т.е. при начальных условиях p₀(0) = 1, p₁(0) = 0, p₂(0) = 0, p₃(0) = 0.

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы p_i(t) в предельном стационарном режиме, т.е. при 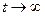, которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния S, имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом, состоянии. Например, если предельная вероятность состояния S₀ т.е. р₀ = 0,5, то это означает, что в среднем половину времени система находится в состоянии S₀.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы S с графом состояний, изображенном на рис. 3.2), такая система уравнений имеет вид:

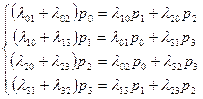(3.3)

Систему (4.3) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния р„ умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в 1-е состояние, на вероятности тех состояний, из которых эти потоки исходят.