Задача Коши. Теорема существования и единственности решения.

Условие, что при 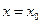функция 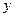должна равняться заданному числу 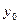, называется начальным условием. Оно записывается в виде .

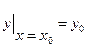Задача отыскания решений дифференциального уравнения, удовлетворяющего начальным условиям, носит название задачи Коши.

Теорема существования и единственности решения.

Для уравнения 1- го порядка справедлива следующая теорема:

Теорема (о существовании и единственности решения дифференциального уравнения первого порядка). Если в уравнении 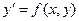функция 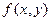и ее частная производная 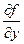непрерывны в некоторой области 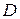на плоскости 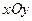, содержащей точку 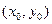, то в некоторой окрестности точки 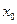существует единственное решение этого уравнения 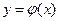, удовлетворяющее условию: при , .

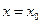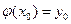Геометрический смысл теоремы заключается в том, что существует и притом единственная функция 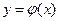, график которой проходит через точку .

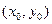Из сформулированной теоремы следует, что уравнение (2) имеет бесконечное число различных решений, ибо через каждую точку области проходит одно решение.