Формула полной вероятности.
Следствием обеих основных теорем- теоремы сложения вероятностей и теоремы умножения вероятностей- является так называемая формула полной вероятности .
Пусть требуется определить вероятность некоторого события A которое может произойти с одним из событий 
, образующих полную группу несовместимых событий .Будем эти события называть гипотезами.
Докажем что в этом случае
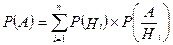

Вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при реализации этой гипотезы.
Эта формула носит название формулы полной вероятности.
Доказательство
Так как гипотезыH1,H2…, Hn,образуетполную группу то событие A может появиться в комбинации с какой либо из этих гиплтез
A=AH1+AH2+…+Ahn.
 |
Т.к.гипотезы Н1, Н2,…,Hn несовместны, то и комбинации Н1А,H2A,…,HnA также несовместны; применяя к нему теорему сложения,получим:

Применяя к событию HiA теорему умножения, получим

Что и требовалось доказать.
Пример.
Имеется три одинаковых на вид урны: в первой урне два белых и один черный шар; во второй-три белых и один черный шар; в третьей-два белых и два черных шара.
Некто выбирает наугад одну из урн и вынимает из нее шар.Найти вероятность того,что этот шар белый.
Решение.
Рассмотрим три гипотезы:
Н1-выбор первой урны,
Н2-выбор второй урны,
Н3-выбор третьей урны
И событие А-появление белого шара.
Т.к.гипотезы по условию задачи равновозможны,то
 |  |
Условные вероятности события А при этих гипотезах соответственно равны


Задача 3.5.
Завод изготовляет изделия, каждое из которых с вероятностью p имеет дефект.
В цехе имеется три контролера; рассматривается только одним контролером, с одинаковой вероятностью первым, вторым или третьим.Вероятность обнаружения дефекта(если оно имеется) для i-го контролера равна Pi (i=1,2,3). Если изделие не было забраковано в цехе, то оно попадает в ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью P0.
Определить вероятность того,что изделие будет забраковано.
Решение.
Пусть
А- изделие будет забраковано
В- изделие будет забраковано в цехе
С- изделие будет забраковано в ОТК завода.
Так как события В и С несовместимы и
А=В+С,то
Р(А)=Р(В)+Р(С)
Находим Р(В).Для того, чтобы изделие было забраковано в цехе, нужно,чтобы оно, во-первых,имело дефект, и во-вторых, чтоб дефект был обнаружен.

Вероятность того,что будет обнаружен дефект в цехе равна
 |
Действительно,
Формулируем гипотезы
Н1-дефект обнаружен 1-ым контролером
Н2-дефект обнаружен 2-ым контролером
Н3-дефект обнаружен 3-им контролером

И

Отсюда

Аналогично


Теорема гипотез (формула Бейеса)
Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез или формула Бейеса.
Поставим следующую задачу.
Имеется полная группа несовместных гипотез Н1,Н2,…Hn.Вероятность этих гипотез до опыта известны и равны соответственно Р(Н1),Р(Н2),…,P(Hn).Произведен опыт,в результате которого наблюдено появление некоторого события А . Спрашивается,как следует изменить вероятности гипотез в связи с появлением этого события?
Здесь по существу, речь идет о том, чтобы найти условную вероятность Р (Hi/A) для каждой гипотезы.
Из теоремы умножения имеем:
P(AHi)=P(A)*P(Hi/A)=P(Hi)*H(A/Hi),
I=1,2,…,n
Или отбрасываем левую часть
P(A)*P(Hi/A)=P(Hi)*P(A/Hi), i=1,2,…,n откуда

Или выражая Р(А) с помощью формулы полной вероятности,имеем

Эта формула и носит название формулы Бейеса или теоремы гипотез
Пример.
Прибор может собираться из высококачественных деталей и из деталей обычного качества;вообще около 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время tравна 0,05; если из деталей обычного качества- его надежность равна 0,7. Прибор испытывается в течении времени t и работал безотказно.Найти вероятность того,что он собран из высококачественных деталей.
Решение.
Возможны две гипотезы:
Н1-прибор собран из высококачественных деталей,
Н2-прибор собран из деталей обычного качества.
Вероятность этих гипотез до опыта
Р(Н1)=0,4; P(H2)=0,6.
В результате опыта наблюдено событие А- прибор безотказно
Работал время t. Условные вероятности этого события при
Гипотезах Н1 и Н2 равны:
P(A/H1) = 0,95 ; P(A/H2) = 0,7 .
По формуле Вейсса находим вероятность гипотезы Н1 после
Опыта :
 |
Задачи комбинаторики.
Во многих статистических исследованиях встречаются комбинаторные задачи, своеобразие которых целесообразно показать на примерах:
Сколькими способами можно расставить на полке 10 различных книг?
В турнире принимают участие 8 команд. Сколько различных представлений относительно трех первых мест (по результатам соревнований) можно сделать?
Сколько различных трехбуквенных слов можно составить из 32 букв алфавита, не обращая внимания на то, имеет ли смысл составленные из букв слова или нет?
Сколькими способами можно из множества k (различных) элементов выбрать r элементов?
Как велико число различных результатов бросаний двух игровых костей .
Приведенные примеры показывают , что в задачах комбинаторики интересуется вообще числом различных выборок определенных объектов , причем , в зависимости от вида дополнительных требований , следует различать , какие выборки считаются одинаковыми и какие различными.
В теории вероятности и математической статистике используют в основном три понятия комбинаторики:
Размещения
Перестановки
Сочетания
Размещениями из n элементов по m называются такие их соединения , которые различаются друг от друга самими элементами или их порядком . Например: размещения из 3 элементов a , b , c по 2: ab, ac, bc, ba, ca, cb.Число всех размещений из n различных элементов по m A
Например: размещения из 3 элементов a , b , c по 2: ab,ac ,bc , ba , ca ,cb.Число всех размещений из n различных элементов по m A

Всего m множителей
Пример:
 |
Перестановками из n элементов называются такие их соединения,отличающиеся друг от друга только порядком входящих в них элементов .Например: перестановка из трех элементов a,b и c: abc, bca, cab , cba, bac, acb. Число всех перестановок из n различных элементов Pn
Pn= 1*2*3* …*n=n!=An
Пример 1:
Пример 2:
Сколькими способами можно расставить на полке 10 книг.
P10=10!=3628800.
Сочетаниями из n элементов по m называются их соединения , различающиеся друг от друга только самими элементами. Например: сочетания из трех элементов a, b и c по два: ab , ac , bc . Число всех сочетаний из n различных элементов по m обозначается Cn


Мы можем записать
Cn=n
Cn = 1
Повторение опытов
При практическом применении теории вероятностей часто приходится встречаться с задачами , в которых один и тот же опыт или аналогичные опыты повторяются неоднократно . В результате каждого опыта может появиться или не появиться некоторое событие А в результате серии опытов.
Такие задачи весьма просто решаются в случае, когда опыты являются независимыми.
Несколько опытов называются независимыми , если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Несколько последовательных выниманий карты из колоды представляет собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются ; в противном случае – зависимые опыты.
Независимые опыты могут производиться в одинаковых или различных условиях .
Общая теорема о повторении опытов.
Частная теорема о повторении опытов касается того случая, когда вероятность события А во всех опытах одна и та же. На практике часто приходится встречаться с более сложным случаем, когда опыты производятся в неодинаковых условиях, и вероятность события от опыта к опыту меняется. Способ вычисления вероятности заданного числа появлений событий в таких условиях дает общая теорема о повторении опытов.
Пусть число опытов u=2, тогда полная группа событий:
P1P2+P1q2+q1P2+q1q2
Пусть число опытов u=3, тогда полная группа событий:
P1P2P3+P1P2q3+P1q2P3+q1P2P3+P1q2q3+q1P2q3+q1q2P+q1q2q3
Аналогично для числа опытов n полная группа событий:
P1P2*…*Pn+P1P2*…*qn+…+q1P2*…*Pn+…+q1*q2*…qn,причем в каждое из произведений событие А входит m раз, а событие А входит n-m раз.Число таких сочетаний по прежнему
 |
но сами комбинации между собой не равновероятны.
Для того, чтобы чисто механически составить все возможные произведения из m букв p и n-m букв q с разными индексами применим следующий формальный прием.Составим произведения n бикомов
jn(z)=(q1+p1z)(q2+p2z)…(qn+pnz)
 |
или короче
где z-произвольный параметр.
Функция jn(z),разложение которой по степеням параметра z дает в качестве коэффициентов вероятности pm,n, называется производящей функцией вероятностей pm,n или просто производящей функцией.
Пользуясь понятием производящий функции, можно сформулировать общую теорему о повторении опытов в следующем виде:

Вероятность того, что событие А в n независимых опытах появится ровно m раз, равна коэффициенту при zm в выражении производящей функции
jn(z)=(qi+piz) где pi-вероятность появления события А в i-ом опыте
qi=1-pi
Вышеприведенная формулировка общей теоремы о повторении опытов в отличии от частной теоремы не дает явного выражения для вероятности pm,n.
Такое выражение в принципе написать можно, но оно является слишком сложным, и мы не будем его приводить.
Однако не прибегая к такому явному выражению, все же можно записать общую теорему о повторении опытов в виде одной формулы
(qi+piz)=pm,nzm
случайная величина.
Одним из важнейших основных понятий теории вероятности является понятие о случайной величине.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое имено.
Примеры случайных величин:
Число вызовов, поступавших на телефонную станцию за сутки;
Количество мальчиков, родившихся в роддоме за месяц;
Количество девочек, родившихся в роддоме за месяц;
Во всех трех примерах случайные величины могут принимать отдельные изолированные значения, которые можно заранее перечислить.
В примере 1;
0,1,2,
Такие случайные величины, принимающие только отдельные, отделенные друг от друга значения называются дискретными величинами.
Существуют случайные величины другого типа.
Например, температура воздуха, влажность воздуха, напряжение в сети электрического тока.
J
Функция распределения.
Ряд распределения, многоугольник распределения не
являются универсальными характеристиками случайной величины:они существуют только для дискретных случайных величин.Нетрудно убедиться,что для непрерывной случайной величины такой характеристики построить нельзя. Действительно, непрерывная случайная величина имеет бесчисленное множество возможных значений, ???? занимающих некоторый промежуток (так называемое “несчетное множество”). Составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Следовательно, для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он существует для прерывной величины. Однако различные области возможных значений случайной величины все же не являются одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для прерывной (или дискретной).
Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события x=x, а вероятностью события x<x, где x некоторая текущая переменая. Вероятность события, очевидно, зависит от x, есть некоторая функция от x.Эта функция называется функцией распределения случайной величины x и обозначается F(x).
 |
Функцию распределения F(x) иногда называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения-универсальная характеристика случайной величины.Она существует для всех случайных величин: как дискретных, так и непрерывных.Функция распределения
Полностью характеризует случайную величину с вероятной точки зрения,т.е. является одной из форм распределения.
Сформулируем некоторые общие свойства функции распределения:
Функция распределения F(x) есть неубывающая функция своего аргумента т.е. при x2>x1 F(x2)>F(x1).
На минус бесконечности функция распределения равна нулю
F(-¥)=0
3.На плюс бесконечности функция распределения равна 1.
F(+¥)=1.
Типичная функция распределения непрерывной случайной величины имеет вид
Вероятность показания случайной величины на заданный участок.
При решении практических задач, связанных со случайными величинами часто оказывается необходимым вычислять вероятность того, что случайная величина примет значение, заключенное в некоторых пределах, например от a до b.
Условимся для определенности левый конец a включать в участок(a,b), а правый-не включать.Тогда попадание случайной величины x на участок(a,b) равносильно выполнено неравенство:
a<x<b
выразим вероятность того события через функцию распределения величины x. Для того рассмотрим три события:
событие А, состоящее в том, что C<b
событие B, состоящее в том, что C<a
событие С, состоящее в том, что a<C<b
Учитывая, что А=В+С, по теореме сложения вероятностей имеем
R(C<b)=R(C<a)+R(a£C<b)
или
F(b)=F(a)+R(a£C<b)
Откуда
P(a£C<b)=F(b)-F(a)
Т.е. вероятность показания случайной величины на заданный предел равна приращению функции распределения на этом участке.
Плотность распределения.
Пусть имеется непрерывная случайная величина x с функцией распределения F(x),которую мы предложим непрерывной и дифференцируемой.
Вычислим вероятность попадания этой величины на участок от x до x+DC:
R(C£C<C+DC)=F(C+DC)-F(x) ,
т.е.приращению функции на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность,приходящуюся на единицу длины на этом участке, и будем приближать DC к 0. В приделе получим производную от функции распределения.
Введем обозначение:

F(x) = F `(x)
Функция f (x)- производная функции распределения - характеризует как бы плотность ,с которой распределяются значения случайной величины в данной точке . Эта функция называется плотностью распределения
(иначе”плотностью вероятности”) непрерывной случайной величины X. Иногда функцию f (x) называют “дифференциальной функцией распределения” или “дифференциальным законом распределения “ величины Х.
Кривая , изображающая плотность распределения случайной величины, называется кривой распределения.
 f(x)
f(x)
Плотность распределения , так же как и функция распределения , есть одна из форм закона распределения.В противоположность от функции распределения эта форма является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную величину Х с плотностью распределения f (x) и элементарный участок DX,
примыкающий к точке Х.

Вероятность нахождения случайной величины Х на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна f (x)dx. Величина f (x)dx называется элементом вероятности . Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx.
Выразим вероятность попадания величины Х на отрезок от a до b через плотность распределения :
Очевидно , она равна сумме элементов вероятности на всем этом участке , то есть интегралу:



Геометрически вероятность попадания величины Х на участке (a,b) равна площади кривой распределения , опирающийся на этот участок .
Формула:
f(x)=F`(x)
выражает плотность распределения через функцию распределения. Зададимся обратрой задачей :выразить функцию распределения через плотность.По определению
F(x)=P(X<x)=P(-¥£X<x)
Откуда по формуле(3) имеем:
 |
F(x)=
Геометрически F(x) есть не что иное,как площадь кривой распределения ,лежащая левее точки:X
Укажем основные свойства плотности распределения:
1.Плотность распределения есть неотрицательная функция
f(x)>³0
Это свойство непосредственно вытекает из того ,что функция распределения F(x) есть неубывающая функция.

2.Интеграл в бесконечных пределах от плотности распределения равен 1
Это следует из того ,что F(+¥)=1
Геометрически основные свойства плотности распределения означают:
1.Вся кривая распределения лежит не ниже оси абсцисс.
2.Полная площадь ,ограниченная кривой распределения и осью абсцисс , равна 1.
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН. ИХ РОЛЬ И НАЗНАЧЕНИЯ .
Мы познакомились с рядом полных характеристик случайных величин- так называемых законов распределения.Такими характеристиками были:
-для дискретной случайной величины
а) функция распределения ;
б) ряд распределения (графически – кривая распределения).
Каждый закон распределения представляет собой некоторую функцию ,и указание этой функции полностью
Описывает случайную величину с вероятностной точки зрения.
Однако во многих вопросах практики нет необходимости характеризовать случайную величину плотностью,исчерпывающим образом .
Зачастую достаточно бывает указать только отдельные числовые параметры , до некоторой степени характеризующие существенные черты распределения
чайной величины : например какое то среднее значение , около группируются возможные значения случайной величины ; какое то число , характеризующее степень разбросанности этих значений относительно среднего , и т. д.
Пользуясь такими характеристиками , мы можем все существенные сведения относительно случайной величины , которыми мы располагаем , выразить наиболее компактно с помощью числовых параметров .Вот эти параметры , которые выражают в сжатой числовой форме наиболее существенные особенности распределения , называются числовыми характеристиками случайной величины .
В теории вероятности и математической статистики применяются большое количество различных числовых характеристик , имеющих различное назначение и различные области применения ,но все они делятся на два класса :
1.Характеристики положения .
2. Характеристики рассеяния .
Характеристики положения.

Математическое ожидание . Медиана . Мода . Начальный момент .
Среди числовых характеристик случайных величин нужно прежде всего отметить те ,которые характеризуют положения случайной величины на числовой оси ,т. е. Указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины .
Из характеристик положения в теории вероятности важнейшую роль играет математическое ожидание случайной величины ,которое иногда называют средним значением случайной величины .
Рассмотрим случайную дискретную величину X , имеющую возможные значения X1,X2 ,…Xn c вероятностями P1, P2 ,… Pn.

Нам требуется характеризовать каким то числом положение значений случайной величины на оси абсцисс . Для этой цели естественно воспользоваться так называемым « «средним взвешенным » из значений Xi, причем каждое значение Xi при ?????????? должно учитываться с «весом» , пропорциональным вероятности этого значения . Т. о. Мы вычислим среднее значение случайной величины x , которое мы обозначим М[x]
 |
 |  |  |
Или учитывая, что
Это среднее взвешенное значение и называется математическим ожиданием случайной величины .
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений с. в . на вероятности этих значений.
Заметим , что в выше приведенной формулировке определение математического ожидания справедлива только для дискретных случайных величин .
 |
Для непрерывной величины x математическое ожидание , естественно выражается уже не суммой , а интегралом :
Где f(x)-плотность распределения случайной величины Х.
F(x)dx-элемент вероятности.
Кроме важнейшей из характеристик положение – математического ожидания, - на практике иногда применяются и другие характеристики положения, в частности мода и медиана
Модой случайной величины называется ее наиболее вероятное значение, строго говоря, применяем только x дискретным величинам
Для непрерывной случайной величины модой является то значение в котором плотность вероятности максимальна
Медианой с. в. X называется такое ее значение Ме , т. е. Одинаково вероятно, окажется ли случайная величина меньше или больше Ме
Геометрически медиана – это абсцисса точки , в которой площадь, ограниченная кривой распределения , делится попалам .
‘ PГрафик функции распределения имеет вид
Задача 5,50
На перекрестке стоит автоматический светофор, в котором
1минуту горит зеленый свет и 0,5 минуты-красный, затем 1 минуту горит зеленый свет,0,5 минут красный и,т,д
некто подъезжает к перекрестку на машине в случайный момент, не связанный с работой
светофора
а) найти вероятность того, что он проедет перекресток не останавливаясь
б)найти среднее время ожидания у перекрестка
Решение
Момент проезда автомашины через перекресток распределен равномерно в интервале , равном
Периоду смены цветов в светофоре
Этот период равен 1+0,5=1,5минут
Для того, чтобы машина проехала через перекресток, не останавливаясь, достаточно, чтобы
Момент проезда перекрестка пришелся на интервал времени (0,1)
Для случайной величены, подчиненный закону постоянной плотности в интервале (0,1,5)
Вероятность того ,что она попадает на интервал (0,1) равна Время ожидания есть смешанная случайная величина ,с вероятностью она равна 0,а с Вероятностью она принимает с одинаковой плотностью вероятности любое значение между 0 и 0,5 минут
Среднее время ожидания у перекрестка
Закон распределения Пуасона
Во многих задачах практики приходится иметь дело со случайными величинами распределенными по своеобразному закону который называется законом пуасона . Рассмотрим
Дискретную величину, которая может принимать только целые неотрицательные значения
0,1,2,..., m,...,
причем последовательность этих значений практически неограничена.
Говорят что случайная величина Х распределена по закону пуасона, если вероятность того , что
Она примет определенные значения m выражается формулой
(m=0.1.2.,,,.m.)
где a- некоторая положительная величина называемая параметром Пуасона.Ряд распределения случайной величины Х , распределенный по закону Пуасона имеет вид ;
 Xm Xm
| ... | m | ... | |||
| Pm |

Дисперсия величины Х равна

Вероятность попадания случайной величины, подчиненной нормальному закону на заданный участок.
Во многих задачах , связанных с нормально распределенными случайными величинами , приходится определять вероятность попадания случайной величины Х , подчиненной нормальному закону с параметрами
m, s,на участок от a до b .
Для вычисления этой вероятности воспользуемся общей формулой.
R (a < C< b) = F( b) – F( a) (1)
где F(b) - функция распределения величины Х в точке b
F(a)-функция распределения величины Х в точке a
Найдем функцию распределения F(x) случайной величины, распределенной по нормальному закону с параметрами m, s. Плотность
распределения величины Х равна:

Отсюда находим функцию распределения :

:
Сделаем в интеграле замену переменной:

И приведем его к виду:

Этот интеграл не выражается через элементарные функции , но для него
составлены таблицы.
Табличная функция распределения (так называемая таблица интеграла вероятностей) обозначается:

Нетрудно видеть, что эта функция представляет собой не что иное , как функцию распределения для нормально распределенной случайной
величины с параметрами m=0; s=1
Функция распределения Ф*(х) называется также нормальной функцией распределения .
Выразим функцию распределения величины Х с параметрами m,s через нормальную функцию распределения:

Теперь найдем вероятность попадания случайной величины Х на участок от a до b .
Согласно формуле (1):

Таким образом , мы выразим вероятность попадания на участок от a до

b случайной величины, распределенной по нормальному закону распределения с любыми параметрами, через стандартную функцию распределения Ф*(х) , соответствующую нормальному закону с параметрами m=0 и s=1. Заметим , что аргументы функции Ф* в последней формуле имеет простой смысл:

есть расстояние от правого конца участка b до центра рассеяния , выраженное в средних квадратических отклонениях;

- есть такое же расстояние для левого конца участка , причем что расстояние считается положительным , если конец расположен справа от центра рассеяния , и отрицательным, если слева.
Как и всякая функция распределения , функция Ф*(х) обладает свойствами:
1.Ф*(- ¥ )=0
2.Ф*(+¥ )=1
3.Ф*(х)- неубывающая функция.
Кроме того, из симметричности нормального распределения с параметрами m=0 и s=1 относительно начала координат следует, что
4.Ф*(-х)=1-Ф*(х).
Рассмотрим следующий пример.
Случайная величина Х , распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния .
При измерении допускается систематическая ошибка в сторону завышения на 1,2(м); среднее квадратическое отклонение ошибки измерения равно 0,8(м).
Найти вероятность того , что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6(м).
Решение.
Ошибка измерения есть случайная величина Х , подчиненная нормальному закону с параметрами m=12 , s=0,8.
Нужно найти вероятность попадания этой величины на участок от
a=--1,б до b= +1,6.
По формуле имеем:

Пользуясь таблицами функции Ф*(0,5)=0,6915 и Ф*(-3,5)=0,0002
Отсюда
Р(-1,6<х<1,6)=0,6915-0,0002=0,6913
Задача 5.48.
Браковка шариков для подшибников производится следующим образом:
если шарик не проходит через отверстие диаметром d2>d1, то его размер считается приемлемым . Если какое- нибудь из этих условий не выполняется, то шарик бракуется . Известно, что диаметр шарика Д есть нормально распределенная случайная величина с характеристиками


Определить вероятность q того, что шарик будет забракован.
Решение.
q= 1- p(d1< d < d2);


Известно, что размер D шарика для подшипника является случайной величиной, распределенной по нормальному закону. Браковка шарика производится так же, как указанно в предыдущей задаче. При этом известно, что средний размер шарика равен

а брак составляет 10% от всего выпуска.Определить среднее квадратическое отклонение диаметра шарика sd.
Решение
Аналогично предыдущей задаче вероятность брака

Откуда
Задача 5-54
Случайная величина х подчинена нормальному закону с математическим мх=0.Вероятность показания этой случайной величины на участках от -1 до 1 равна 0.5.
 |
Найти среднее квадратичное отклонение и написать выражение нормального закона

Откуда четность распределения

Построим график функции четность распределения
| x | -5 | -4 | -3 | -2 | -1 | ||||||
| -5,68 | -3,64 | -2,05 | -0,91 | -0,22 | -0,22 | -0,91 | -2,05 | -3,64 | -5,68 | ||
| 0,003 | 0,026 | 0,129 | 0,403 | 0,803 | 0,803 | 0,403 | 0,129 | 0,026 | 0,003 | ||
| 0,001 | 0,01 | 0,03 | 0,11 | 0,22 | 0,3 | 0,22 | 0,11 | 0,03 | 0,01 | 0,001 |
Здесь должен быть график
Задача 5-58.
Имеется случайная величина х , подчиненная нормальному закону е математическим ожиданием мх, а средним квадратичным отклонением сигма от х . Требуется приближенно
Заменить нормальный закон законом постоянной плотности в интервале альфа, бета; границы альфа, бета подобрать так, чтобы сохранить неизменными основные характеристики случайной величины х: математическое ожидание и дисперсию.
 |
Решение

Решая эту систему уравнений относительно альфа и бета

Ответ

СЛУЧАЙНАЯ ВЕЛИЧИНА Х ПОДЧИНЕНА НОРМАЛЬНОМУ ЗАКОНУ С МАТЕМАТИ-ЧЕСКИМ ОЖИДАНИЕМ Мх=3. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СЛУЧАЙНОЙ ВЕЛИЧИ-НЫ НА УЧАСТОК ОТ 2 ДО 4 РАВНА 0,5. НАЙТИ СРЕДНЕЕ КВАДРАТИЧНОЕ ОТ-КЛОНЕНИЕ И НАПИСАТЬ ВЫРАЖЕНИЕ НОРМАЛЬНОГО ЗАКОНА. ПОСТРОИТЬ ГРА-ФИК ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ.


 |
ОТКУДА ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ

ПОСТРОИМ ГРАФИК ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
| Х | -2 | -1 | |||||||||
| -5,68 | -3,64 | -2,05 | -0,91 | -0,22 | -0,22 | -0,91 | -2,05 | -3,64 | -5,68 | ||
| 0,0033 | 0,0262 | 0,1287 | 0,4025 | 0,8025 | 0,8025 | 0,4025 | 0,1287 | 0,0262 | 0,033 | ||
| 0,001 | 0,01 | 0,03 | 0,11 | 0,22 | 0,270 | 0,22 | 0,11 | 0,03 | 0,01 | 0,001 |
Вариант 2
 |
Случайная величина Х подчинена нормальному закону с математиче-ским ожиданием Мх=6. Вероятность попадания этой случайной величины на участок от 4 до8 равна 0,6. Найти среднее квадратичное отклонение и написать выражение нормального закона. Построить график плотности распределения.

Откуда плотность распределения
Построим график плотности распределения.
| х | -1 | ||||||||||||||
| -4,36 | -3,04 | -2,20 | -1,35 | -0,76 | -0,34 | -0,08 | -0,08 | -0,34 | -0,76 | -1,35 | -2,20 | -3,04 | -4,36 | ||
ПРАВИЛО ТРЕХ s
Пусть нормальная величина Х распределена по нормальному закону с параметрами М и s. Ппокажем что с точностью до 03% случается величина подчиненная закону принимает возможные значения не отклоняющиеся от центра рассеяния на ± 3s.
Мы хотим найти что

Не превысит 0003

Правило 3s в статистике имеет большое значение.
Одно из самых распространенных правил 3s - это отсеивающий экспери-мент. При отсеивающем эксперименте производят отсеивание выбросов.
Основные задачи математической статистики
Дата добавления: 2016-11-26; просмотров: 3053;











