Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
Сначала дадим понятие решения уравнения (3).
Определение 1.Решением уравнения (3) на отрезке 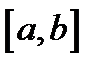 называется такая функция
называется такая функция
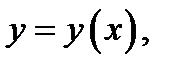 которая удовлетворяет следующим условиям:
которая удовлетворяет следующим условиям:
1) функция 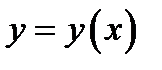 дифференцируема
дифференцируема 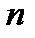 раз на указанном отрезке;
раз на указанном отрезке;
2) точка 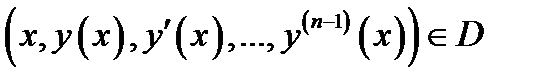 при всех
при всех 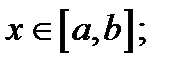
3) имеет место тождество 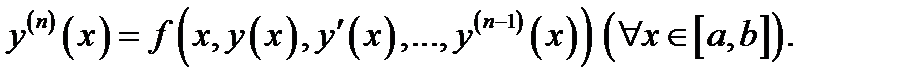
Например, функция 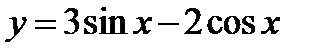 является решением уравнения
является решением уравнения 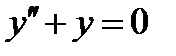 на всей оси
на всей оси 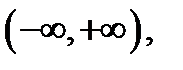 так как имеет место тождество
так как имеет место тождество 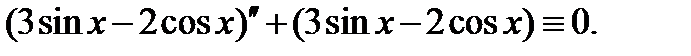
Начальная задача (задача Коши) для уравнения (1) ставится следующим образом:

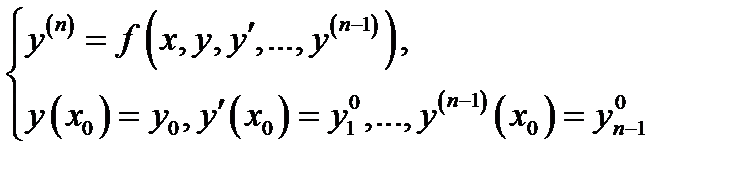
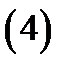
и формулируется так: для фиксированной начальной точки 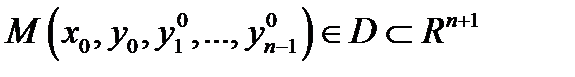 найти решение
найти решение 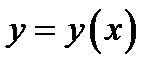 уравнения (3), график которого (интегральная кривая) проходит через точку
уравнения (3), график которого (интегральная кривая) проходит через точку 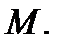 Имеет место следующее утверждение.
Имеет место следующее утверждение.
Теорема Коши(существования и единственности решения начальной задачи для уравнения высшего порядка). Пусть в уравнении (3) функция 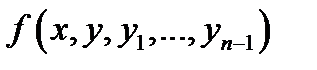 и её частные производные
и её частные производные 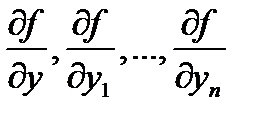 непрерывны в области
непрерывны в области 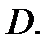 Тогда какова бы ни была начальная точка
Тогда какова бы ни была начальная точка 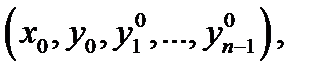 лежащая внутри области
лежащая внутри области 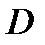 , существует число
, существует число 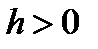 такое, что задача Коши (4) с указанной начальной точкой имеет на отрезке
такое, что задача Коши (4) с указанной начальной точкой имеет на отрезке 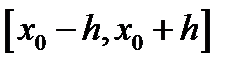 решение
решение 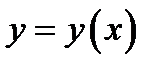 и это решение единственно на указанном отрезке.
и это решение единственно на указанном отрезке.
Обращаем внимание на достаточный и локальный характер этой теоремы (см. предыдущую лекцию). Так же, как и в случае уравнения первого порядка, здесь вводятся понятия частного и общего решений (и их интегралов).
Определение 2.Частным решениемуравнения (3) называется решение какой-нибудь его задачи Коши (4). Общим решением уравнения (3) в области 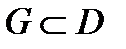 называется функция
называется функция 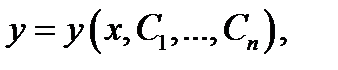 зависящая от
зависящая от 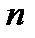 произвольных постоянных
произвольных постоянных 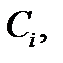 удовлетворяю-
удовлетворяю-
щая следующим условиям:
1) при любых допустимых значениях постоянных 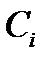 функция
функция 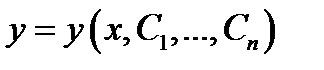 является решением уравнения (1) на некотором отрезке
является решением уравнения (1) на некотором отрезке 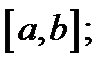
2) какова бы ни была начальная точка 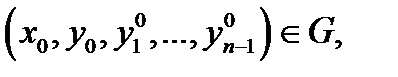 существуют значения постоянных
существуют значения постоянных 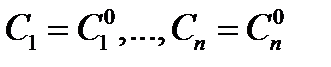 такие, что функция
такие, что функция 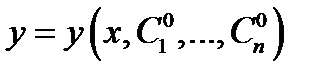 является решением задачи Коши (4) с этой начальной точкой.
является решением задачи Коши (4) с этой начальной точкой.
И, наконец, частный интеграл уравнения (3) есть частное решение этого уравнения, записанное в неявной форме 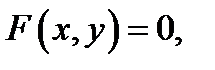 а общий интеграл суть общее уравнения (3), записанное в неявной форме
а общий интеграл суть общее уравнения (3), записанное в неявной форме 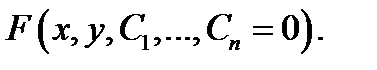
Для проверки того, что соотношение 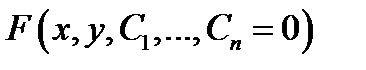 является общим интегралом уравнения (3) надо из системы уравнений
является общим интегралом уравнения (3) надо из системы уравнений
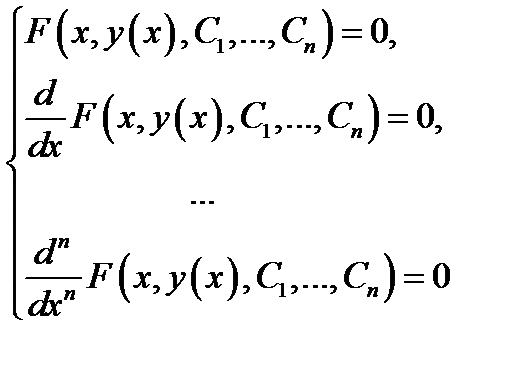
исключить произвольные постоянные 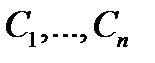 . Если при этом будет получено дифференциальное уравнение (3) (или эквивалентное ему уравнение), то
. Если при этом будет получено дифференциальное уравнение (3) (или эквивалентное ему уравнение), то 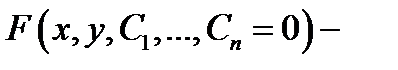 общий интеграл этого уравнения. Предлагаем в качестве упражнения проверить, что соотношение
общий интеграл этого уравнения. Предлагаем в качестве упражнения проверить, что соотношение 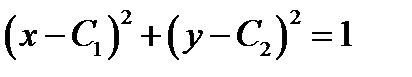 является общим интегралом уравнения
является общим интегралом уравнения 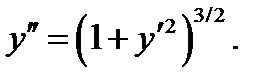
Дата добавления: 2016-06-05; просмотров: 2602;











