Вступ до синтезу алгоритмів шифрування. Операції з шифрами по Шеннону. Теорема Маркова

У підсумку аналізу захищених (безпечних) систем, що застосовують криптографічні перетворення, американський інженер Клод Шеннон зробив висновок про можливість використання для їх побудови двох простих операції комбінування, за допомогою яких з двох початкових систем створюють третю.

Перша операція комбінування отримала назву множення та відповідає шифруванню повідомлення спочатку системою 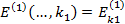, а потім 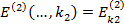, при цьому ключі шифрів обираються незалежно.

Результат операції представляє криптографічну систему:

,

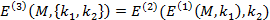або:

.

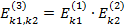Ймовірність кінцевого відображення є результатом множення ймовірностей вихідних відображень.

Друга комбінована операція, що отримала назву зваженого додавання, може бути подана у вигляді:

,

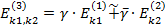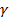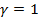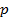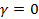де – випадкова величина, яка приймає значення з ймовірністю або з ймовірністю 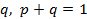. Суть перетворення полягає у наступному, якщо 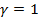, застосовується результат перетворення 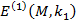, в іншому випадку .

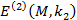Очевидно, що у підсумку операції множення двох однотипних перетворень може бути отримане перетворення цього типу. Зокрема, застосування двох різних простих замін еквівалентно дії іншої простої заміни. Аналогічно, результат двократної перестановки вихідного тексту еквівалентний застосуванню перестановки, що має довжину, яка є найменшим спільним кратним довжин двох перших.

Розгляд проблем синтезу та аналізу криптосхем в деяких випадках уявляється доцільним розглядати на рівні їх автоматних моделей. Зокрема, побудова автоматної моделі для криптографічних модулів є обов’язковим елементом вимог федерального стандарту США FIPS 140-2/