Теорема сложения вероятностей.
Теорема сложения вероятностей формулируется следующим образом:
Вероятность суммы двух несовместных равна сумме вероятностей этих событий:
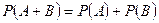 .
.
Докажем теорему сложения вероятностей для схемы случаев.
Пусть возможные исходы опыта сводится к совокупности случаев, которые мы для наглядности изображения в виде n точек

ЗДЕСЬ ДОЛЖЕН БЫТЬ РИСУНОК.
n - число случаев (всех шаров в уравнении)
m - число случаев благоприятных событию А (число красных шаров)
к - число случаев благоприятных событию В (число зеленых шаров)
Найти вероятность события
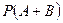 ,
,
что будет вынут цветной шар.
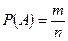 ;
;
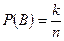 .
.
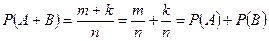
Аналогично эту теорию можно доказать для 3,4 ... n вероятностей.
Для сложения n вероятностей формула имеет вид
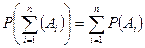
Теорема имеет 2 следствия:
Следствие 1. Если события 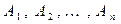 образуют полную группу несовместных событий, то сумма их вероятностей равна единице
образуют полную группу несовместных событий, то сумма их вероятностей равна единице
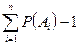
Доказательство.
Т.к. события 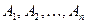 образуют полную группу событий, то появление хотя бы одного из них – достоверное событие,
образуют полную группу событий, то появление хотя бы одного из них – достоверное событие,
т. е. 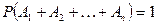 .
.
Из теории сложения вероятностей :
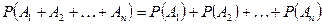
Откуда
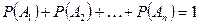 .
.
Перед тем как вывести второе следствие теоремы сложения, определим понятие о противоположных событиях.
Противоположными событиями называются два несовместных события, образующих полную группу.
Примеры противоположных событий:
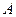 - выпадение герба при бросании монеты;
- выпадение герба при бросании монеты;
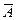 - выпадение решки
- выпадение решки
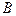 - выпадение не более 5 очков при бросании кости
- выпадение не более 5 очков при бросании кости
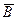 – выпадение 6 очков
– выпадение 6 очков
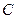 - безотказная работа всех элементов технической системы
- безотказная работа всех элементов технической системы
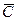 - выход хотя бы одного элемента технической системы
- выход хотя бы одного элемента технической системы
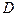 – в парти не выявлено не одного бракованного изделия
– в парти не выявлено не одного бракованного изделия
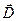 - в партии имеется хотя бы одно бракованное изделие
- в партии имеется хотя бы одно бракованное изделие
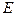 - обнаружение не менее двух бракованных изделий в контрольной партии
- обнаружение не менее двух бракованных изделий в контрольной партии
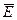 Е- обнаружение не более одного бракованного изделия
Е- обнаружение не более одного бракованного изделия
Следствие 2. Сумма вероятностей противоположных событий равна 1.
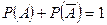 .
.
Это следствие есть частный случай следствия 1. Оно выделено ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события 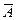 чем вероятность прямого события
чем вероятность прямого события 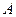 . И этих случаях вычисляют
. И этих случаях вычисляют 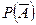 и находят
и находят 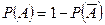 .
.
Дата добавления: 2016-11-26; просмотров: 1738;











