Принятия решений без использования вероятностей исходов
Рассмотрим частный случай предложенной выше модели задачи в условиях неопределенности. Предположим, что каждому возможному состоянию среды соответствует один возможный исход.
Таким образом, в данном случае математическая модель задачи принятия решений определяется множеством стратегий Х = {хi}, множеством состояний среды S = {Sk}, а также следующей матрицей полезности (матрицей доходов)
| Sj xi | S1 | S2 | ¼ | Sn |
| x1 | f11 | f12 | ¼ | f1n |
| x2 | f21 | f22 | ¼ | |
| ¼ | ¼ | ¼ | ¼ | ¼ |
| xm | fm1 | fm2 | ¼ | fmn |
L =
где fij = u(Sj,хi). Существует несколько критериев для выбора оптимальной стратегии.
Критерий Вальда (правило максимина - критерий осторожного наблюдателя) Этот критерий оптимизирует полезность (доход) в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. По данному критерию решающее правило имеет следующий вид
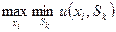
Напомним, что наблюдателю неизвестно распределение вероятностей p(Sk). Относительно состояния среды наблюдатель может высказывать определенные гипотезы. Его предположения о вероятном состоянии среды называются субъективными вероятностями.
По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния среды.
Критерий Гурвица (компромиссный способ принятия решений) основан на следующих двух предположениях: среда может находиться в самом невыгодном состоянии с вероятностью (1 - a) и в самом выгодном - с вероятностью a, где a - коэффициент доверия (параметр риска).
Тогда решающее правило записывается так
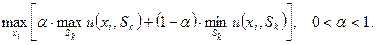
Если a = 0, получаем критерий Вальда. Если a = 1, то приходим к решающему правилу максимакса, то есть к так называемой стратегии "здорового оптимиста" (называемую иногда "подходом карточного игрока"), который верит в удачу и, игнорируя возможные потери, рассчитывает на максимально возможный доход
Критерий Сэвиджа (правило минимакса - критерий минимизации максимально возможных потерь, минимизации "сожалений"). "Сожаление" - это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния.
Чтобы определить "сожаление", в каждом столбце матрицы полезности (доходов) находят максимальный элемент Uk, затем вычитают его из всех элементов этого столбца. Таким образом получают матрицу "сожалений", каждый элемент которой представляет собой разность
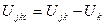
где Ujk - элементы исходной матрицы полезности (доходов).
Искомую стратегию хi , которая минимизирует "сожаление" (возможные потери или упущенный доход), определяют из условия
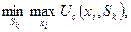
где 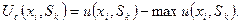
Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшим образом отличается от предполагаемого.
Рассмотрим использование описанных критериев в условиях неопределенности для практической ситуации
Пример. Фирма "Крона" решает построить отель в одном из курортных мест Необходимо определить наиболее целесообразное количество мест или комнат в этой гостинице.
Составляют смету расходов по строительству гостиницы с различным количеством комнат, а также рассчитывают ожидаемый доход в зависимости от количества комнат, которые будут сняты.
В зависимости от принятого решения - количества комнат в гостинице х = 20, 30, 40, 50-и количества снятых комнат S = 0, 10, 20, 30, 40, 50, которое зависит от множества случайных факторов и неизвестно фирме, получают следующую таблицу ежегодных прибылей (в тыс. долл.)
| Sk хi | ||||||
| -121 | ||||||
| -168 | ||||||
| -216 | -33 | |||||
| -264 | -81 |
Наиболее подходящее количество комнат в гостинице определим по вышеприведенным критериям.
Критерий Вальда:
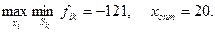
Судя по результатам, критерий Вальда неприменим, так как в этом случае от постройки гостиницы следует отказаться.
Критерий Гурвица:
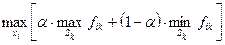
Для разных a можно построить таблицу доходов по критерию Гурвица:
| a | 0,1 | 0,2 | 0,5 | 0,9 |
| -84 | -47 | |||
| -114 | -59 | |||
| -143 | -70 | |||
| -172 | -81 |
Тогда оптимальное количество комнат в гостинице, в соответствии с критерием Гурвица, в зависимости от a:
| a | 0,1 | 0,2 | 0,5 | 0,9 |
| xопт |
Критерий Сэвиджа. Построим матрицу "сожалений".
| Sk хi | ||||||
| -135 | -270 | -405 | ||||
| -47 | -48 | -47 | -135 | -275 | ||
| -95 | -95 | -95 | -48 | -135 | ||
| -145 | -143 | -144 | -96 | -47 |
В соответствии с приведенным выше критерием Сэвиджа получим
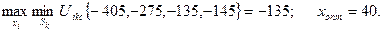
Таким образом, предстоит сделать выбор между различными решениями
· по критерию Вальда строить 20 комнат,
· по критерию Гурвица строить 20 комнат если заказчик - пессимист, и 50 комнат, если он оптимист,
· по критерию Сэвиджа следует строить 40 комнат.
Какое из возможных решений предпочтительнее, определяется выбором соответствующего критерия. Выбор критерия является наиболее сложным и ответственным этапом. При этом не существует каких-либо общих рекомендаций или советов. Выбор критерия должен производить управленец на соответствующем уровне и в максимальной степени согласовывать этот выбор с конкретной спецификой задачи, а также со своими целями.
В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем, и заказчик намерен вложить в проект столько средств, чтобы потом он не сожалел, что вложено слишком мало, то выбирают критерий Сэвиджа.
При отсутствии достаточной информации для выбора того или иного критерия возможен альтернативный подход, который связан с вычислением шансов на успех и разорение на основе прошлого опыта.
Принятие решений с учетом вероятностей состояния среды
Здесь рассмотрим правила принятия решений с использованием численных значений вероятностей исходов. Эта задача возникает в том случае, когда с каждой принимаемой стратегией х, связано целое множество (а не один) возможных результатов O1, O2, . . . , Оn с известными вероятностями 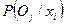 .
.
Формально модель задачи может быть представлена в виде следующей матрицы
| Oj xi | O1 | O2 | ¼ | Oj | ¼ | On |
| x1 | f11 | f12 | ¼ | f1j | ¼ | f1n |
| x2 | f21 | f22 | ¼ | f2j | ¼ | f2n |
| ¼ | ¼ | ¼ | ¼ | ¼ | ¼ | ¼ |
| xi | fi1 | fi2 | ¼ | fij | ¼ | fin |
| ¼ | ¼ | ¼ | ¼ | ¼ | ¼ | ¼ |
| xm | fm1 | fm2 | ¼ | fmj | ¼ | fmn |
где fik - полезность результата Oj при использовании решения xi .
При известных вероятностях 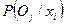 используют два подхода к принятию решений.
используют два подхода к принятию решений.
1. Правило максимальной вероятности - максимизация наиболее вероятных доходов. При этом в приведенной матрице доходов выбирают элементы, имеющие наибольшие вероятности исходов и среди этих элементов выбирается тот, который имеет наибольший доход. Рассмотрим эту задачу на примере
Пример. Предположим, что вы, читатель, являетесь владельцем небольшой кондитерской "Сластена" В начале каждого дня вам нужно решить вопрос, сколько пирожных следует иметь в запасе, чтобы удовлетворить спрос. Каждое пирожное обходится вам в 2 грн. , а продаете вы его по 3 грн. Продать невостребованные пирожные на следующий день невозможно, поэтому остаток распродается в конце дня по 1 грн. за штуку. В таблице приведены данные по продажам в предыдущие периоды
| Спрос на пирожные в день (в сотнях штук) | |||||
| Частота | |||||
| Относительная частота (вероятность) | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Нужно определить, сколько пирожных должно быть закуплено в начале каждого дня.
Прежде чем использовать какое-либо правило принятия решения, рассчитаем матрицу полезности, описывающую величины дохода (в гривнах) для всех комбинаций возможных исходов (дневного спроса пирожных) и решений (числа закупленных для продажи пирожных)
| Возможные исходы спрос пирожных в день (в сотнях шт ) | Возможные решения число закупленных для продажи пирожных (в сотнях штук) | ||||
| -100 | -200 | -300 | |||
| -100 | |||||
При использовании правила максимальной вероятности выберем исходы с наибольшей вероятностью. Наибольшая вероятность 0,3 соответствует спросу в 300 и 400 пирожных в день. Теперь рассмотрим доходы каждого из решений при этих исходах. Больший доход (400 грн) соответствует количеству закупаемых пирожных, равному 400 штук, когда возможный исход равен 400 шт и больше. Таким образом, фирма "Сластена" должна закупать 400 пирожных в день
2.Оптимизация математического ожидания. Этот способ использования вероятностей при принятии решения является наиболее распространенным.
Решающее правило для определения оптимальной стратегии xi в этом случае записывается так
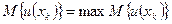
где 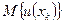 - математическое ожидание дохода для каждого исхода.
- математическое ожидание дохода для каждого исхода.
Математическое ожидание рассчитывается для каждого решения либо для доходов, либо для возможных потерь. Выбирается решение либо с наибольшим ожидаемым доходом, либо с наименьшими возможными потерями.
Вернемся к примеру о пирожных, закупаемых фирмой "Сластена". Ниже приведена таблица доходов, дополненная вероятностями каждого из исходов
| Возможные исходы спрос пирожных в день (в сотнях шт ) | Возможные решения число закупленных для продажи пирожных (в сотнях штук) | Вероят-ность | ||||
| -100 | -200 | -300 | 0,1 | |||
| -100 | 0,2 | |||||
| 0,3 | ||||||
| 0,3 | ||||||
| 0,1 |
Рассчитаем математическое ожидание дохода для каждого решения
| Возможные исходы спрос пирожных в день (в сотнях шт ) | Возможные решения число закупленных для продажи пирожных (в сотнях штук) | ||||
| -10 | -20 | -30 | |||
| -20 | |||||
| Ожидаемый доход в день всего, грн |
Итак, максимальное значение ожидаемого дохода составляет 220 грн. в день, следовательно, используя критерий максимизации математического ожидания дохода, фирма "Сластена" должна закупать ежедневно триста пирожных.
Аналогично определяется оптимальная стратегия на основе минимизации математического ожидания возможных потерь.
Дата добавления: 2016-11-26; просмотров: 2839;











