Алгоритм Фокса умножения матриц
Пусть А и В - квадратные матрицы порядка n, а р - общее число процессоров. Ниже рассмотрим следующие вопросы:
1. случай р = n2
2. блочная реализация (р < n2)
3. пример работы Fox's алгоритма
Случай р = n2
В данном случае получается, что каждому процессору назначается по одному элементу от каждой из матриц А, В и С. Распределим элементы матриц между процессорами следующим образом. Процессору с номером i*n+j (в дальнейшем процессору (i, j)) назначим элементы матриц А, В и С, находящиеся в i-той строке и j-том столбце. Здесь i, j изменяются от 0 до n-1. В данном частном случае Fox's алгоритм будет выполнять умножение матриц А и В за n этапов. Примем, что начальный этап имеет номер 0, а последний этап номер n-1. Тогда на начальном этапе процессор(i, j) умножает диагональный элемент матрицы А на элемент 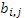 матрицы В, а результат умножения помещает в элемент матрицы С:
матрицы В, а результат умножения помещает в элемент матрицы С:
этап 0 для процессора (i, j): Су = * 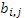
Процессор (i, j) будет иметь доступ к элементу матрицы А за счет того, что процессоры обмениваются данными между собой. Вопросы обмена данными будут рассмотрены позднее.
Перед тем как рассматривать следующий этап, введем понятие деления по модулю n:
i mod n = i, если i < n
i mod n = i % n, если i > = n (i % n - остаток от деления i на n )
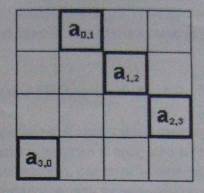
Теперь перейдем непосредственно к рассмотрению следующего этапа. На первом этапе процессор (i, j) умножает элемент матрицы А на элемент 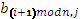 матрицы В. Результат умножения складывается со значением элемента начального этапа, и полученная сумма снова помещается в элемент матрицы С. Следует сказать, что элемент матрицы А - это элемент, стоящий непосредственно справа от диагонального элемента , если i принимает значение от 0 до n- 2, и элемент равен элементу , если i = n-1. На рисунке элементы показаны для случая, когда п = 4.
матрицы В. Результат умножения складывается со значением элемента начального этапа, и полученная сумма снова помещается в элемент матрицы С. Следует сказать, что элемент матрицы А - это элемент, стоящий непосредственно справа от диагонального элемента , если i принимает значение от 0 до n- 2, и элемент равен элементу , если i = n-1. На рисунке элементы показаны для случая, когда п = 4.
Аналогично элемент 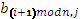 матрицы В - это элемент стоящий на одну строчку ниже в отличии от элемента
матрицы В - это элемент стоящий на одну строчку ниже в отличии от элемента 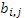 этапа 0, если i принимает значение от 0 до n-2, и элемент
этапа 0, если i принимает значение от 0 до n-2, и элемент 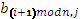 равен элементу
равен элементу 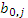 , если i = n-1.
, если i = n-1.
этап 1 для процессора (i,j): = + * 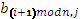
В общем случае, во время k-ого этапа процессор (i, j) выполняет умножение элемента матрицы А на элемент 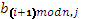 матрицы В, и складывает результат умножения с элементом предыдущего этапа. Обозначим через к сумму (i+k) mod n, тогда этап к для процессора (i, j) будет выглядеть следующим образом:
матрицы В, и складывает результат умножения с элементом предыдущего этапа. Обозначим через к сумму (i+k) mod n, тогда этап к для процессора (i, j) будет выглядеть следующим образом:
этап k для процессора (i, j): = + * 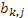
После выполнения последнего этапа Fox's алгоритма элемент будет представляться в виде следующей суммы:
= * 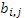 + *
+ * 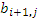 +...+ *
+...+ * 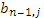 + *
+ * 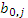 +...+ *
+...+ * 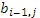
А эта сумма есть ничто иное как сумма произведений элементов i-той строки матрицы А на элементы j-того столбца матрицы В. Таким образом, можно сделать вывод о том, что Fox's алгоритм для перемножения квадратных матриц порядка n и числа процессоров р = n2 работает правильно.
Блочная реализация (р < n2)
Очевидно, что при решении практических задач требование р = n2 является трудно выполнимым. Так, при умножении двух матриц порядка n = 100 уже требуется 10 000 процессоров. Естественным решением проблемы является назначение процессорам не отдельных элементов, а квадратных подматриц порядка n/(р1/2) от каждой из матриц А, В и C. В этом случае Fox's алгоритм будет выполнять умножение матриц А и В за р1/2 этапов. На каждом этапе процессор (i, j) будет получать подматрицу 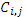 , формула для вычисления которой имеет вид, аналогичный формуле для вычисления элемента
, формула для вычисления которой имеет вид, аналогичный формуле для вычисления элемента 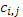 матрицы C, с той лишь разницей, что вместо элементов и
матрицы C, с той лишь разницей, что вместо элементов и 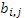 следует использовать подматрицы и
следует использовать подматрицы и 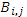 и i, j будут изменяться от 0 до р1/2 -1. В этом случае этап k для процессора (i, j) будет иметь следующий вид:
и i, j будут изменяться от 0 до р1/2 -1. В этом случае этап k для процессора (i, j) будет иметь следующий вид:
этап k для процессора (i, j): 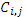 =
= 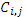 + *
+ * 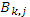
Единственной проблемой при таком подходе является отсутствие какой либо гарантии в том, что n/(р1/2) будет целым числом. Основная сложность состоит в неизвестности порядка матриц n, т.к. р1/2 можно сделать целым числом, если из общего числа процессоров взять только то число, из которого извлекается корень, а оставшиеся процессоры будут просто неработающими. Трудности, связанные с порядком матриц могут быть преодолены за счет введения недостающих строк и столбцов, заполненных нулевыми элементами. В дальнейшем будем полагать, что n/(р1/2) - целое число.
Дата добавления: 2016-05-31; просмотров: 3163;











