Линейная производственная функция

Пример 3. Линейная ПФ (ЛПФ) имеет вид 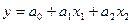(двухфакторная) и 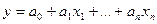(многофакторная), ЛПФ принадлежит к классу аддитивных ПФ (АПФ). Переход от мультипликативной ПФ к аддитивной осуществляется с помощью операции логарифмирования.

Для двухфакторной мультипликативной ПФ

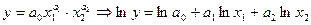
Пусть lny=w, lnx₁=v₁, lnx₂=v₂ получим аддитивную ПФ

.

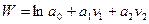Выполняя обратный переход, из аддитивной ПФ получим мультипликативную ПФ.

Если сумма показателей степени в ПФ Кобба - Дугласа y, 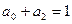, то её можно записать в другой форме:

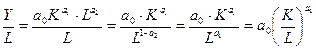, то есть

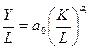
Пусть 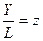производительность труда,

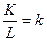- капиталовооружённость труда,

Тогда 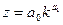, то есть из двухфакторной ПФКД получим формально однофакторную ПФКД.

Так как 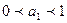, из последней формулы следует, что производительность труда z растёт медленнее капиталовооруженности труда.

Этот случай справедлив для случая статической ПФКД в рамках существующих технологий и ресурсов.

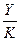- производительность капитала, или капиталоотдача

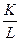- капиталоёмкость выпуска

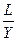- трудоёмкость выпуска.

ПФ называется динамической, если:

1 Время t фигурирует в качестве самостоятельной переменной величины или фактора производства, влияющего на объём выпускаемой продукции;

2 Параметры ПФ и её характеристика f зависят от времени t.

При построении ПФ научно-технический прогресс (НТП) может быть учтён с помощью введения множителя НТП е^pt, где t = 0,1,…, T

Эта ПФ – простейший пример динамической ПФ, она включает нейтральный, то есть не материализованный в одном из факторов, технический прогресс.

В более сложных случаях технический прогресс может воздействовать непосредственно на производительность труда или капиталоотдачу:

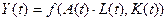или

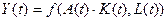
НТП называется в этом случае трудосберегающим или капиталосберегающим.