Простейшая модель равновесия.

В экономической теории важным является понятие равновесия, то есть такого состояния объекта, которое он сохраняет при отсутствии внешних воздействий. Задачи экономической динамики включают как описание процессов выхода к состоянию равновесия, так и процессов трансформации самого этого состояния под воздействием внешних сил.

Дифференциальное уравнение связывает изменения показателя x(t) или просто х со скоростью его движения 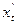или х^’. Будем считать, что скорость изменения показателя х пропорциональна величине его отклонения от равновесного значения х_е. Чем дальше показатель отклонился от равновесного значения, тем быстрее он стремится вернуться к нему. Если в уравнении присутствует только первая производная х по времени, а сама связь линейна, то это линейное дифференциальное уравнение.

Пусть х`=k∙(х-х<sub>е</sub>), где k- коэффициент, kх<sub>е</sub>- сводный член; без него уравнение х`=k∙х- называется однородным и его решение х=С∙l^kt.

Исходное неоднородное уравнение имеет частное решение х=х_е (если величина х находится в состоянии равновесия), а общее его решение есть сумма любого частного решения и общего решения однородного уравнения, т.е.

x = х_е +С∙l^kt.

При t=0 величина х=х(0) получаем С=х(0)-х_е и х(t)= х_е+(х(0)-х_е)e^kt.

1.) При k < 0, e^kt→0 и равновесие устойчиво, то есть при отклонении величины х(t) от значения х_е она вновь стремиться принять это значение.

2.) При k > 0, величина e^kt→∞ и соответственно х(t) стремится к бесконечности (если начальное состояние не совпадает с состоянием равновесия)

1) k <0 2) k >0 0

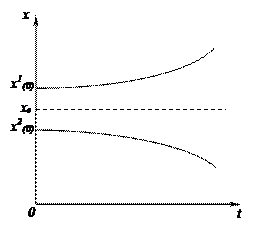
Рис. 9 Рис. 10

Система выходит к состоянию х_е на Рис. 9.

Ее поведение при k>0 показано на Рис.10.

Рис. 11 Рис. 12

Поведение динамических систем может также описываться графиками

Рис. 11 и Рис. 12.

Поведение в дискретном времени может быть описано с помощью разностного уравнения, связывающего величины х в соседние моменты времени, т.е. х_t и x_t-1.

Например, в дискретной ситуации, аналогично уже рассмотренной, может использоваться разностное уравнение:

х_t = x_t-1+ к(x_t-1 – х_е),

решением его является:

х_t = x_е+ (x(0) – х_е)(1+k)^t.

Это решение может быть найдено (аналогично непрерывному случаю) как сумма общего решения 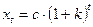для однородного уравнения 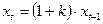и частного решения 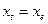для исходного разностного уравнения; с учетом 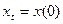, при t = 0.

1). При k < 0 система в случае отклонения от x_е будет двигаться в направлении x_е,

2). При k > 0 уходит еще дальше от него.

1). Равновесие устойчиво при – 2 < k < 0.

2). Неустойчиво при k > 0 или k = –2.

3). При k < –1 показатель х каждый раз «перескакивает» равновесное значение x_е при чем при k < –2 – слишком далеко, чтобы приблизиться в конце концов к x_е.