Производственная функция Кобба-Дугласа

<10 11 12 13 141516 >

Зависимости в уравнении производственной функции от затрат труда и капитала окажут помощь начинающему трейдеру в достижении результатов на рынке форекс.
Идея производственной функции была впервые предложена американским экономистом П. Дугласом и математиком Ч. Коббом в 1928 г. в виде функции в которой фигурируют только два фактора: затраты труда и капитала. Эта упрощенная форма (в которой не учитываются затраты природных ресурсов) получила большое распространение в силу трудностей учета затрат природных ресурсов, и лишь в последние годы начали предприниматься попытки учесть вклад всех трех факторов.
В 30-е гг. голландский экономист Ян Тинберген (ставший впоследствии Нобелевским лауреатом) показал, что параметр, характеризующий технологию производства, меняется во времени.

Согласно оценкам Тинбергена, сделанным им для нескольких стран на период 1870—1914 гг., в Германии экстенсивные факторы обеспечили 60% роста, интенсивные (технический прогресс) — 40; в Великобритании — соответственно 80 и 20, в США —73 и 27%.

http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-0580.htm

Экономико-математический словарь КОББА-ДУГЛАСА ФУНКЦИЯ [Cobb-Douglas production function] - производственная функция, примененная американскими исследователями Ч. Коббом и П. Дугласом при анализе развития экономики США в 20-30-х гг. ХХ века. Имеет простую алгебраическую форму: N = A · L^α K^β, где N - национальный доход; A - коэффициент размерности; L и K - соответственно объемы приложенного труда и капитала; α и β - константы (коэффициенты эластичности производства по труду L и капиталу K). Функция - однородная степени α+β; следовательно, увеличение L и K в одинаковое число раз m увеличивает доход в m^α+β раз. Если сумма α+β равна единице - функция линейно однородная; если больше или меньше единицы, имеет место эффект масштаба (соответственно положительный или отрицательный). К.-Д. ф. основывается на предположениях о понижающейся предельной отдаче ресурсов (см. Закон убывающей отдачи, Предельный эффект затрат), постоянстве коэффициентов эластичности производства по затратам ресурсов. Эластичность замещения ресурсов в любой точке кривой К.-Д. ф. равна единице. Хотя К.-Д. ф. нельзя отнести к линейным, значения параметров А, α, β можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов. Для этого ее приводят к линейному виду, прологарифмировав обе части уравнения (обычно здесь берутся натуральные логарифмы): lnN = ln А + α lnL + β lnK . Модификация функции, учитывающая технический прогресс, достигается введением дополнительного сомножителя e^π, где π - темп технического прогресса (константа).

http://www.sseu.ru/edumat/v_mat/gloss/g330.htm

Типичным примером производственной функции степенного вида является функция Кобба - Дугласа. В 1928 г. Ч. Кобб и

П. Дуглас на основе данных по обрабатывающей промышленности США за период 1899 - 1922 гг. представили функцию

Р = bL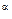K,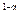

где Р - расчетный индекс производства; К - индекс основного капитала; L - индекс занятости. Это была первая эмпирическая производственная функция, построенная по данным временных рядов.

Определение. Производственная функция Кобба - Дугласа устанавливает зависимость величины созданного общественного продукта от совокупных затрат живого труда 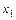и суммарного объема применяемых производственных фондов 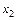. Она имеет следующий вид:

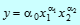где 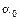- коэффициент, учитывающий влияние факторов, не вошедших в это уравнение, их конкретные числовые значения определяются на основе статистических данных с помощью корреляционных методов, соблюдаются условия .

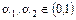Хотя каждый из коэффициентов меньше 1, их сумма может быть меньше, равна или больше 1. Эта сумма показывает эффект одновременного пропорционального увеличения объема как ресурсов труда, так и производственных фондов.

http://nit.miem.edu.ru/cgi-bin/article?id=122

<10 11 12 13 141516 >

Дата добавления: 2021-02-19; просмотров: 289;