Динамического моделирования.

Эта модель позволяет исследовать устойчивость цен и объемов товаров на рынке, описываемом традиционными кривыми спроса и предложения при наличии запаздывания во времени (лага).

Рис. 13

Пусть производители определяют предложение товара в текущем периоде на основе цен, установившихся в предшествующем периоде, т.е.

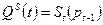
Таким образом, в функцию предложения вклинивается временной лаг продолжительностью в одну единицу времени.

Решение об объеме производства принимается с учетом текущих цен, но производственный цикл имеет определенную продолжительность, и соответствующее этому решению предложение появится на рынке по окончании данного цикла.

Кривая спроса характеризует зависимость объема спроса на товар от цены товара в данном периоде, т.е.

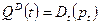
Таким образом, динамику цены можно описать системой уравнений:

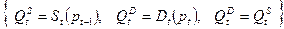
или одним уравнением:

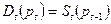
Из этого уравнения можно найти 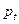в текущий момент времени по известному значению 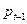в предшествующий момент времени.

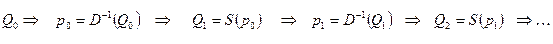
где 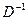– обратная функция спроса.

В качестве частного случая рассмотрим паутинообразную модель, в которой спрос и предложение линейны:

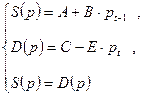
Здесь В > 0 , т.к. функция предложения возрастающая;

Е > 0, т.к. функция спроса убывающая 0 < A < C , или 0 < С(0) < D(0)

Будем считать, что при нулевой цене спрос превышает предложение.

Уравнение, описывающее динамику такой системы, имеет вид

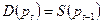или

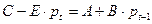
Найдем сначала равновесную цену 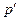и равновесный объем 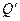, они должны удовлетворять уравнениям:

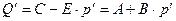отсюда

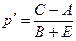и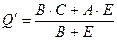

Далее необходимо исследовать поведение цен и объемов производства в том случае, если начальная точка не совпадает с равновесной.

Эту задачу можно решить графическим, получив рисунок типа «паутины». Задав некоторое первоначальное количество товара и цену, не совпадающие с точкой равновесия, будем последовательно наносить точки в соответствии с процедурой расчета по модели, соединяя их горизонтальными и вертикальными прямыми.

Из графического анализа можно получить следующие результаты:

1). 2).

Рис.14 Рис.15

3).

Рис. 15

1). Если кривая предложения наклонена круче, чем кривая спроса, то равновесие на таком рынке будет устойчивым.

2). Если кривая спроса наклонена круче, чем кривая предложения, то равновесие на рынке будет неустойчивым.

3). При равном наклоне кривых спроса и предложения цены на рынке будут испытывать регулярные колебания с постоянной амплитудой.

Перейдем к формальному анализу модели.

Выражая, 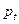через 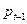имеем, следующее рекуррентное соотношение:

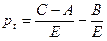
Последовательно применяя это соотношение, находим:

;

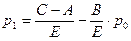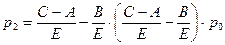
Или в общем виде

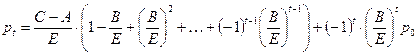
Выражение в скобках есть сумма геометрической прогрессии:

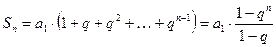
Если 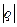< 1 то 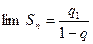, при n→∞.

Для паутинообразной модели , .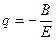

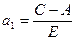Отсюда получаем выражение для цены 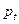в произвольный момент времени t:

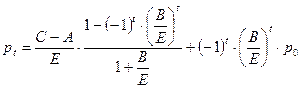
Очевидно: пр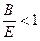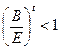и ; ; и 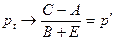, т.е. при более крутом наклоне кривой предложения, чем кривой спроса, равновесие является устойчивым.

1). Если 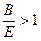, то есть более крутой является кривая спроса, то 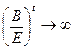и процесс расходится (равновесие неустойчиво).

2). При 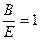, т.е. 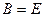значения 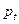чередуются вокруг равновесного значения.

Выводы. Определяющим моментом для устойчивости системы является менее сильная, сглаживающая реакция на изменения цены той функции, которая имеет временной лаг (В нашем случае это функция предложения).

В реальности при 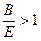бесконечно возрастающих колебаний не будет, т.к. при больших отклонениях от равновесия линейное приближение становится не реалистичным. В более реалистической нелинейной модели устанавливаются нелинейные колебания большой, но конечной амплитуды, которые являются прообразом экономических циклов подъема и спада производства.

Задача. Имеется паутинообразная модель

; ; .

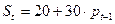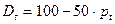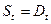Пусть 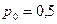, чему равно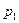

Решение

Т.к. 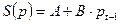то А = 20; В = 30

и 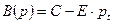то С = 100; Е = 50

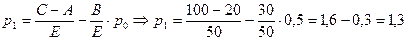
Дополнительные главы к курсу.