Производственная функция вида Кобба - Дугласа

Пример 2.Для моделирования отдельного региона или страны в целом часто используются ПФ вида 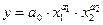, где а₀ , а₁ , а₂ – параметры ПФ. Это положительные постоянные, часто а₁ и а₂ 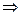а_{1 +} а₂ = 1.

ПФ приведенного вида называется ПФ Кобба-Дугласа (ПФКД) по имени двух американских экономистов (1929г).

ПФКД активно используется для решения разнообразных теоретических и прикладных задач благодаря своей структурной простоте.

ПФКД принадлежит к классу мультипликативных ПФ(МПФ).

В приложениях ПФКД:

х₁ =K- объём используемого основного капитала (объём используемых основных фондов),

х₂₌ L- затраты живого труда.

Тогда ПФКД примет вид:

.

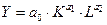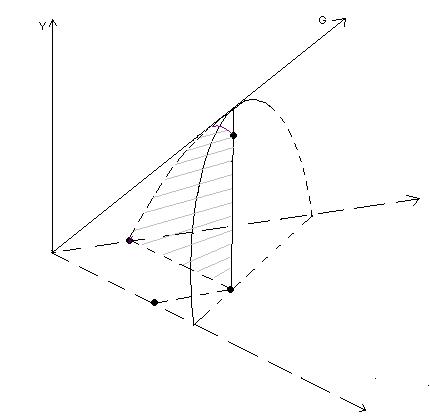Графиком ПФ 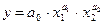, (а₁+а₂=1) в трехмерном пространстве является двумерная поверхность G, эскиз который представлен на рисунке 5.

g

(x_1,x⁰_2,y)

x₂

x⁰₂

(x_1,x⁰₂)

x₁

x₁

рис.5

График G в рассматриваемом случае есть коническая поверхность, направляющей которой является линия L, а образующими - лучи, выходящие из точки 0.

Пусть 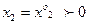, тогда 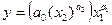и мы получаем вариант ПФ, аналогичный рассмотренному на рис. 4 и на рис. 6.

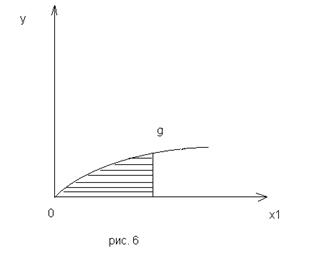
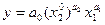
Линия g есть пересечение поверхности G вертикальной плоскостью. .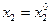

На рис. 6 представлен фрагмент рис. 5, относящийся к линии g.

Поведение линии g отражает то обстоятельство, что с ростом затрат первого ресурса объём выпуска y растёт, но каждая дополнительная единица первого ресурса обеспечивает всё меньший прирост выпуска y.

Это обстоятельство можно интерпретировать так: если число работников и их квалификация остаются неизменными, а число обслуживаемых ими станков увеличивается, например, в два раза, то это не приведёт к двойному росту объёма выпуска.

Если 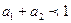, то графиком функции G ПФКД является поверхность, которая напоминает выпуклую вверх «горку», крутизна которой падает, если точки 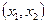перемещается на «северо-восток» по плоскости .