Формальные свойства производственных функций.

Производственная функция f(x₁, x₂) как формальна конструкция определена в неотрицательной ортанте двухмерной плоскости, то есть определена при .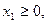

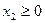ПФ должна удовлетворять ряду свойств (для каждой конкретной ПФ).

1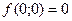

1^'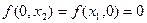

2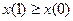

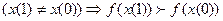
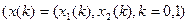
2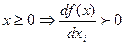^' (i = 1,2; х = (х₁, х₂))

3 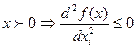(i = 1,2; х = (х₁, х₂))

3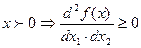^' х = (х₁, х₂)

4 .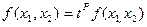

Свойство 1) означает, что без ресурсов нет выпуска;

свойство 1^' означает, что при отсутствии хотя бы одного из ресурсов нет выпуска;

свойство 2 означает, что с ростом затрат хотя бы одного ресурса объём выпуска растёт;

свойство 2^' (частная производная ПФ 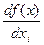положительна) означает, что с ростом затрат одного ресурса при неизменном количестве другого ресурса объём выпуска растёт. Упорядоченная пара (х₁, х₂) чисел для краткости обозначается символом х, то есть х = (х₁, х₂);

свойство 3 означает, что с тостом затрат одного (i-го) ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не растёт (закон убывающей эффективности);

свойство 3' означает, что при росте одного ресурса предельная эффективность другого ресурса возрастает.

Если выполнены условия 3 и 3', то график G ПФ – есть поверхность, расположенная в неотрицательном ортанте 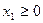, , 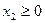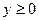трёхмерного пространства 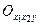и выпуклая вверх.

Вообще геометрический образ ПФ должен прежде всего ассоциироваться с выпуклой горкой, крутизна которой убывает, если точка (х₁, х₂) уходит в плоскости 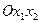на «северо-восток».

Свойство 4 означает, что ПФ является однородной функцией (ОФ) степени .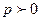

При 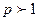с ростом масштаба производства в t раз (число 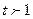), то есть с переходом от вектора х к вектору tx, объём выпуска возрастёт в 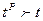раз, то есть имеем рост эффективности производства от роста масштаба производства.

При 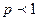имеем падение эффективности производства от роста масштаба производства.

При 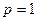имеем постоянную эффективность производства при росте его масштаба (или имеем независимость удельного выпуска от масштаба производства).

Для ПФКД

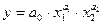_, если 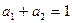Свойства 1-4 выполняются.

Для ЛПФ

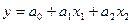если ,

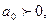
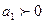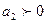
Свойства 1 и 1' при а_о = 0 и свойство 4 не выполняются.

Множество (линия) l_q уровня 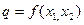, где 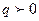, действительное число y ПФ 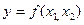, называется изоквантой ПФ, или по-другому: линия уровня q - это множество точек, в котором ПФ постоянна и равна q.

Различные наборы 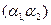b 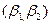затрачиваемых (используемых) ресурсов, принадлежащие одной и той же изокванте l_q (то есть 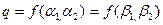) дают один и тот же объём выпуска q.

Изокванта есть линия, расположенная в неотрицательной оранте 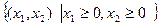двухмерной плоскости .

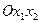Пример

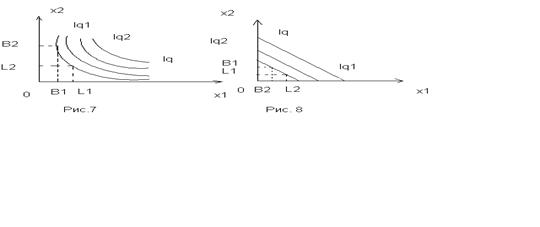
На Рис. 7 даны эскизы изоквант l_q1 и l_q2 ПФКД. Отметим, что изокванта l_q2 расположенная северо-восточнее изокванты l_q1 соответствует большему объёму выпуска (то есть 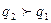). Если объём используемого основного капитала неограниченно растёт, то есть 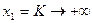, то, как видно из рис. 7, затраты труда неограниченно убывают, то есть 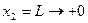, аналогично, как видно на рис. 7, если 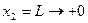, то .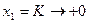

На рис. 8 даны эскиз изоквант l_q1 и l_q2 ( )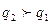

При n = 2 для любой ПФ, для которой справедливы все, или часть, свойств 1-4, изокванта (если она не является прямой) есть линия, не обязательно гладкая, которая выпукла в точке О, то есть которая похожа на изокванту lq рис. 7. Если график G ПФ похож на выпуклую горку, то, естественно, что её изокванты есть линии, выпуклые к точке О.